This morning, I attended an engaging virtual workshop on modelling and applications of evolutionary game theory.

I extend my sincere thanks to the organisers – Alex McAvoy, Olivia Chu, and Daniel Cooney (bsky) – for their kind invitation and organising the workshop. The presentations in my session were all very interesting.

Maria Kleshnina's talk

Maria Kleshnina presented an overview of her recent work on iterated games. I’m particularly intrigued by her model where player behaviour receives feedback from the environment, which I’ve previously discussed on my blog here. She also discussed the concept of endowment distributions and sharing rules that are resilient to variation in the continuation probability. I’ve recently been studying the latter through her manuscript.

Anuraag Bukkuri's talk

Anuraag Bukkuri presented a model for cancer-cell dynamics using a stage-structured adaptive dynamic approach. While I’ve done a little work using the adaptive-dynamics framework, my focus has been on traditional eco-evolutionary applications. I had no idea that it could also be used to design more effective cancer treatments, which was a wonderful thing to learn.

Dini Wang's talk

Dini Wang (Github, manuscript presented) presented an exploration of evolutionary games on hypergraphs. While there’s extensive literature studying the evolution of cooperation on networks, hypergraphs have received comparatively less attention. A hypergraph extends the concept of a simple graph: rather than players being connected solely through pairwise edges, they form potentially overlapping groups. These group relationships can be represented by hyperedges, which are edges capable of connecting more than two nodes simultaneously.

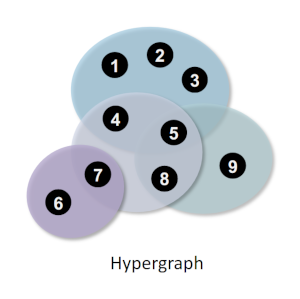
An example of a hypergraph, taken from Dini's manuscript. The nodes numbered 1-9 are players, and their group-connection is indicated by the shaded regions.

An example of a hypergraph, taken from Dini’s manuscript. The nodes numbered 1-9 are players, and their group-connection is indicated by the shaded regions.

The hypergraph structure influences both the payoffs players receive and the strategy-update process in evolutionary dynamics. For example, if you belong to two groups, you participate in two games, with your overall payoff being a combination from both games. Hypergraphs also allow for more possibilities in the strategy-updating process than a regular graph. For example, in the social-learning dynamics, when choosing which high-payoff individual to imitate, one might first select an outstanding group and then randomly select an individual from within this group.

Dini comprehensively explored different combinations of update rules made possible by the hypergraph structure, and she presented findings on which structures promoted cooperation and which updating rules were most effective (details in her manuscript). I was particularly struck by her discovery that, compared to simple graphs, the higher-order interactions facilitated by hypergraph structures are more conducive to cooperation. This was my first introduction to hypergraphs, and they appear to offer a more natural framework for describing human interactions than pairwise connections, so I’m excited to read her manuscript in more detail.

Saptarshi Pal's talk

Finally, Saptarshi Pal presented on different conceptualisations of resilience in subgame perfect Nash equilibria as they relate to symmetric 2-player, 2-strategy iterated games. His work focused on infinite iteration (continuation probability \(\delta = 1\)) and memory-1 strategies. All of these concepts are new territory for me, which means my interpretations of them below are likely wrong — please ask him for his manuscript to be sure.

The first concept was the resilient strategy, which strengthens the notion of a SPNE. When both players adopt such a strategy, at no point in the game does any player have an incentive to deviate. Or, to put it another way, the strategy is independent of the history that has occurred up to this point, and the condition being met is robust to variation in that history.

The second concept was the stably resilient strategy, which maintains its resilience even when the game’s payoffs are perturbed. This can be viewed as a strategy that remains a best response even when players face uncertainty about exact payoffs. Interestingly, it appears that virtually every resilient strategy is also stably resilient, and the set of stably resilient strategies consists of just four types: self-cooperators, self-defectors, and two forms of alternators.

The final concept was the most intriguing — the prediction-proof strategy — which is a strategy that remains resilient even against opponents who can anticipate the player’s next move. While “seeing the future” might seem far-fetched, Saptarshi provided the real-world example of tennis champion Andre Agassi, who gained an advantage over Boris Becker by noticing that Becker unconsciously signalled the direction of his serves with his tongue. It seems likely we broadcast many signals about our intentions, both consciously and unconsciously.

As a concrete example, consider the coordination game with payoffs \((R, S, T, P) = (1, 0, 0, 1)\), where everyone ideally wants to play CC or DD. Flipping a coin is a resilient strategy if one’s partner only looks at history. However, if they have a strategy that conditions on your future move, then their deviation payoff is higher (1 > 1/2), and so this SPNE is not a prediction-proof strategy. The concept of a prediction-proof strategy is also applicable to situations where the stage game is not simultaneous because the follower “predicts” what the leader has done by having already seen it.

Saptarshi showed that these strategy types form a nested hierarchy: stably resilient \(\subseteq\) prediction proof \(\subseteq\) resilient \(\subseteq\) SPNE. In addition, the stably resilient strategies (or one of them?) are socially optimal, having the maximum total payoffs of all memory-1 games. This clean result allows for a clear definition of the optimal strategy. Saptarshi plans to extend this work to scenarios where \(\delta < 1\).

My talk

I presented an overview of my recent work developing mathematical techniques for analysing the evolution of cooperation in group games with family members. My slides are available here.