Filed Under #macroecology
Jan 1, 2022
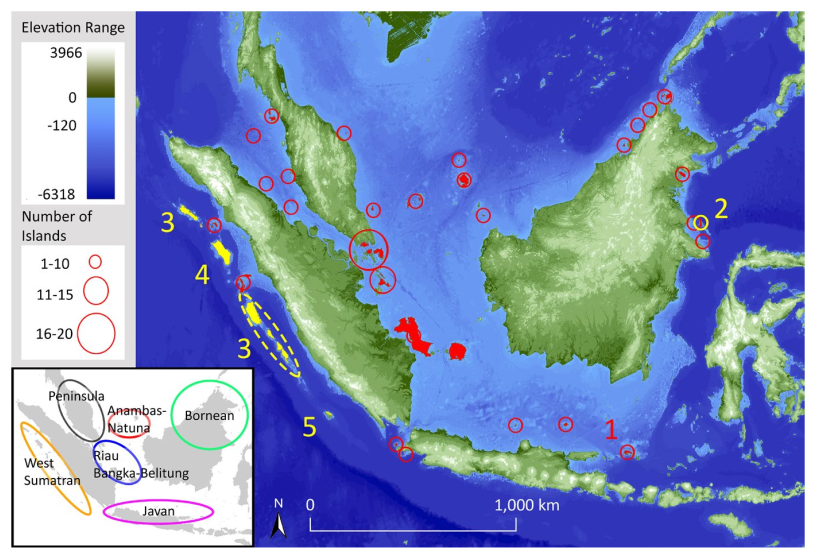The number of species on an island generally increases with island size and connectance to the mainland. However, if an island’s characteristics have changed in the recent past, that pattern will be disrupted. In Keita Sin’s recent paper in Journal of Biogeography, we tested if that expectation was borne out for birds on the Sundaic islands. Perhaps surprisingly, we found that it was not. The number of species on an island is generally determined by immigration and extinction (MacArthur & Wilson, 1967). Over long timescales, these two forces reach a stochastic equilibrium, producing the well-known species-richness patterns. Larger islands permit...
Island bird diversity not influenced by historical connection to the mainland
The number of species on an island generally increases with island size and connectance to the mainland. However, if an island’s characteristics have changed in the recent past, that pattern will be disrupted. In Keita Sin’s recent paper in Journal of Biogeography, we tested if that expectation was borne out for birds on the Sundaic islands. Perhaps surprisingly, we found that it was not. The number of species on an island is generally determined by immigration and extinction (MacArthur & Wilson, 1967). Over long timescales, these two forces reach a stochastic equilibrium, producing the well-known species-richness patterns. Larger islands permit...
Sep 29, 2021
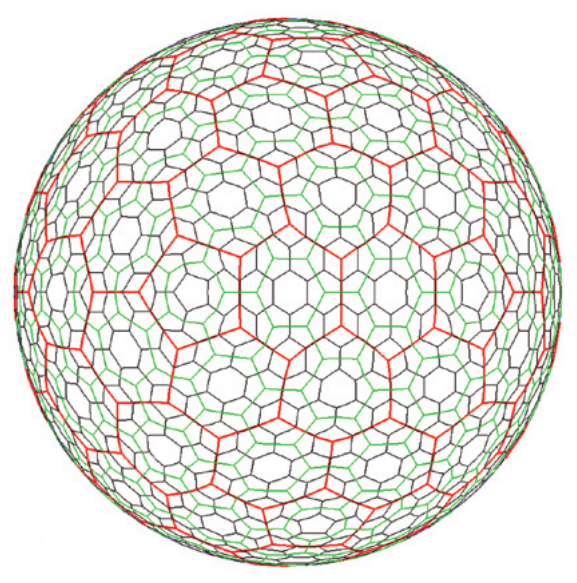In order to model a spatially discretised process on the whole Earth, we need a discrete global grid system (DGGS). Ideally, the DGGS would divide the globe into a tessellation of some regular polygon, analogous to a grid of squares on the plane, where the grid resolution can be increased by further subdivision of the polygon. Another desirable property would be to have equal-distant centres, such as a hexagonal grid, so that the neighbourhood of a grid cell is well defined. Unfortunately, it is not possible to tessellate a sphere with hexagons only, and there are mathematical limits to e.g....
Finding cell neighbours in an ISEA3H global grid in dggridR
In order to model a spatially discretised process on the whole Earth, we need a discrete global grid system (DGGS). Ideally, the DGGS would divide the globe into a tessellation of some regular polygon, analogous to a grid of squares on the plane, where the grid resolution can be increased by further subdivision of the polygon. Another desirable property would be to have equal-distant centres, such as a hexagonal grid, so that the neighbourhood of a grid cell is well defined. Unfortunately, it is not possible to tessellate a sphere with hexagons only, and there are mathematical limits to e.g....
Jul 16, 2021
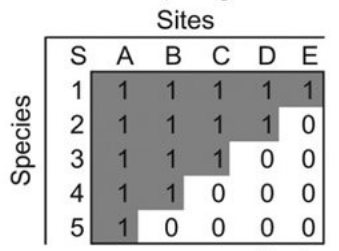The purpose of this blog post is to work through the example in Almeida-Neto et al. (2008) for calculating the NODF nestedness metric. We’re interested in a species-site presence-absence matrix, which is a binary matrix with rows corresponding to species, columns corresponding to sites, and the presence of a species at a site represented by a 1. In a perfectly nested matrix, the sets of species at the sites and the sets of sites at which a species is present form proper subsets of each other. The figure below shows an example of a perfectly nested matrix. An example of...
NODF nestedness worked example
The purpose of this blog post is to work through the example in Almeida-Neto et al. (2008) for calculating the NODF nestedness metric. We’re interested in a species-site presence-absence matrix, which is a binary matrix with rows corresponding to species, columns corresponding to sites, and the presence of a species at a site represented by a 1. In a perfectly nested matrix, the sets of species at the sites and the sets of sites at which a species is present form proper subsets of each other. The figure below shows an example of a perfectly nested matrix. An example of...
Nov 1, 2020
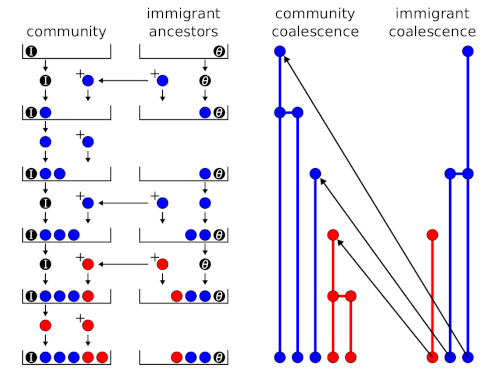A random sample of a species abundance distribution from a neutral metacommunity can be generated using a sequential sampling scheme or urn model (Etienne, 2005, 2007). An urn model is an idealised systems where some objects of actual statistical interest are represented as colored balls in an urn. In the ecological context, the balls represent individuals, the different colours are different species, and the urn’s final state represents the sample. I posted previously about the sequential sampling scheme that is used to generate a random sample from a neutral metacommunity. Hubbell (2001) called it a ‘species generator’, but the concept...
Sequential sampling schemes (urn models) for neutral ecological models
A random sample of a species abundance distribution from a neutral metacommunity can be generated using a sequential sampling scheme or urn model (Etienne, 2005, 2007). An urn model is an idealised systems where some objects of actual statistical interest are represented as colored balls in an urn. In the ecological context, the balls represent individuals, the different colours are different species, and the urn’s final state represents the sample. I posted previously about the sequential sampling scheme that is used to generate a random sample from a neutral metacommunity. Hubbell (2001) called it a ‘species generator’, but the concept...
Sep 8, 2020
Where does Hubbell's 'species generator' come from?
On page 289 onwards, Hubbell (2001) gives an algorithm for sequentially sampling individuals from the neutral metacommunity and obtaining their species identities. The algorithm makes use of a quantity he calls the ‘species generator’ \[\frac{\theta}{\theta + j - 1}\] where \(\theta\) is the “fundamental biodiversity number” and \(j\) is the index of the individual drawn (1st, 2nd, …). In Figure 9.1 he gives a flow diagram for the algorithm, but it is perhaps easier to understand from reading code directly. From the hubbell package for R, Jari Oksanen authored this code: function(theta, J) { community <- NULL for (j in...Feb 22, 2020
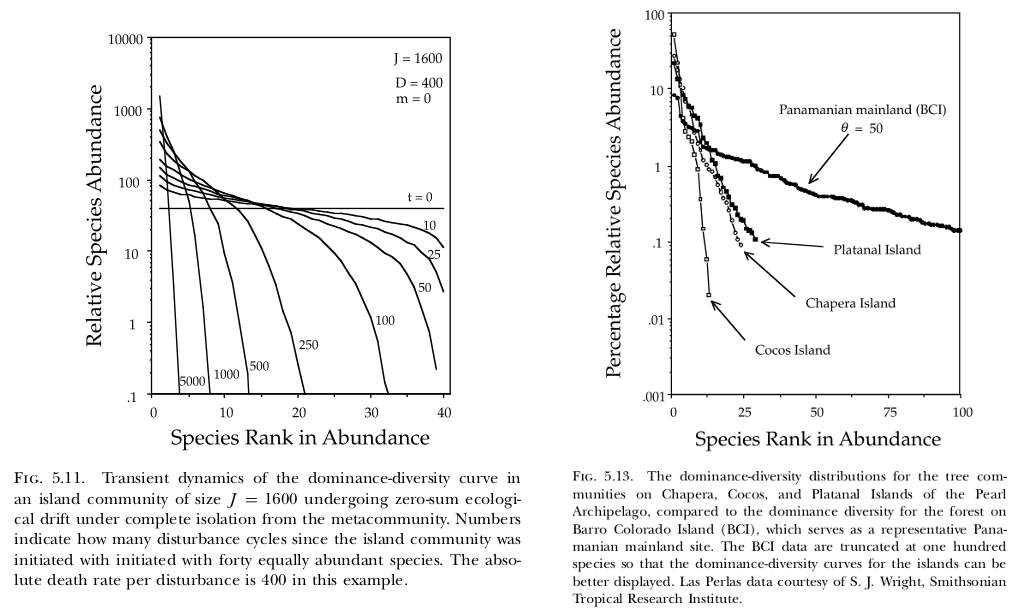In their 10-year-anniversary review of neutral theory (Hubbell, 2001), Rosindell et al. (2011) note that little work has been done on the model’s transient dynamics. Transient dynamics are nonetheless interesting because they can capture important processes occurring in recently disturbed landscapes. For example, if forest is cleared such that only a small patch remains, then the number of species in that patch will continue to decline over time (i.e. extinction debt). As another example (Hubbell, 2001, p. 140–142), the Pearl Archipelago in the Bay of Panama was once a continuous coastal plain attached to the mainland. As the water rose...
Transient dynamics in neutral models
In their 10-year-anniversary review of neutral theory (Hubbell, 2001), Rosindell et al. (2011) note that little work has been done on the model’s transient dynamics. Transient dynamics are nonetheless interesting because they can capture important processes occurring in recently disturbed landscapes. For example, if forest is cleared such that only a small patch remains, then the number of species in that patch will continue to decline over time (i.e. extinction debt). As another example (Hubbell, 2001, p. 140–142), the Pearl Archipelago in the Bay of Panama was once a continuous coastal plain attached to the mainland. As the water rose...