Filed Under #food_webs
Dec 28, 2021
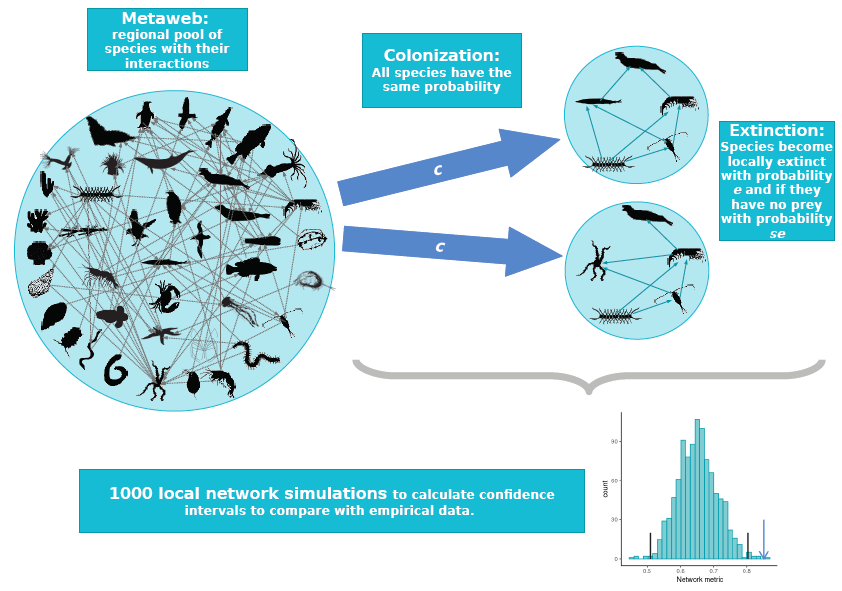What determines the structure of a food web? It has long been theorised that food-web assembly is a selective process, allowing only certain species and interactions to persist in the face of dynamical stability constraints. In Leo Saravia’s recent paper in Journal of Animal Ecology, we used a novel test to see if we could detect the signal of this selection. We compared the structure of real food webs to those of webs randomly assembled from the regional metaweb. Contrary to theoretical expectations, we found almost no difference between them. Figure 1: The null food-web assembly model. Species randomly colonise...
Little difference between real food webs and randomly assembled webs
What determines the structure of a food web? It has long been theorised that food-web assembly is a selective process, allowing only certain species and interactions to persist in the face of dynamical stability constraints. In Leo Saravia’s recent paper in Journal of Animal Ecology, we used a novel test to see if we could detect the signal of this selection. We compared the structure of real food webs to those of webs randomly assembled from the regional metaweb. Contrary to theoretical expectations, we found almost no difference between them. Figure 1: The null food-web assembly model. Species randomly colonise...
Dec 15, 2015
Fibonacci numbers and alternating signs in species responses to press perturbation in a food chain
In a paper from 2001, Dambacher and Rossignol made a curious observation: Fibonacci numbers appear in the adjoint and absolute feedback matrices that result from a weighted-predictions matrix type analysis (Dambacher et al. 2003) on food chains. The weighted-predictions matrix analysis is a way of predicting how species in a food web will respond to a the press perturbation of one of the species, so that implies that the pattern of species response to certain kinds of disturbance follows a neat mathematical pattern. To understand where these Fibonacci numbers come from, a paper by Usmani (1994) is useful. First some...Mar 30, 2012
Stability in large webs
Allesina & Tang (2012 Nature): An extension of analytic, Wigner semicircle theorem-like, stability criteria to predator-prey, competition and mutualism cases. Finds predator-prey interactions permit stability in networks as large and complex as real ones. Hierarchy is: competition-mutualism mixture, random, predator-prey. Finds that stability is less likely when both predator-prey networks and mutualistic networks are given more realistic structure (i.e. niche-model structure and nestedness respectively).Feb 16, 2012
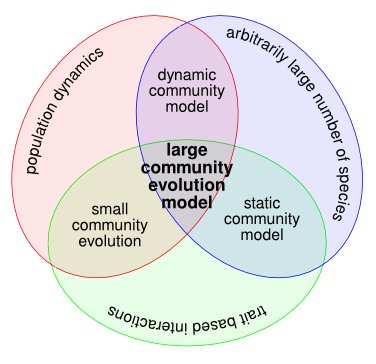Several reviews exist on the influence of evolution on food-web structure (Yoshida, 2006; Fussman et al., 2007; Loeuille & Loreau, 2009; Loeuille, 2010). In Brannstrom et al. (2008), we reviewed past theoretical modelling efforts to study food web structure, and the current state of large community evolution models to tackle the problem. Schematic illustration of the community models that were considered in our review. We started out by surveying static and dynamic ecological models, which do not possess an evolutionary component. After this, we moved on to evolution in small community models. Finally, we reviewed large community-evolution models, which synthesise...
Large community evolution models
Several reviews exist on the influence of evolution on food-web structure (Yoshida, 2006; Fussman et al., 2007; Loeuille & Loreau, 2009; Loeuille, 2010). In Brannstrom et al. (2008), we reviewed past theoretical modelling efforts to study food web structure, and the current state of large community evolution models to tackle the problem. Schematic illustration of the community models that were considered in our review. We started out by surveying static and dynamic ecological models, which do not possess an evolutionary component. After this, we moved on to evolution in small community models. Finally, we reviewed large community-evolution models, which synthesise...
Jan 3, 2012
Link distribution in static community models like the niche model
I was recently reading a 2006 review of food web structure by Jennifer Dunne, which includes a very thorough discussion of static community models like the niche model (Williams & Martinez 2000, Nature), and I was struck again by how unclear it is - to me, anyway - what exactly it is that these static models represent. There’s no doubt that they do an excellent job of replicating the coarse structural properties of large empirical food webs. They also provide important concrete evidence that food web structure is non-random, and a set of simple rules that replicate this structure …...Jun 6, 2011
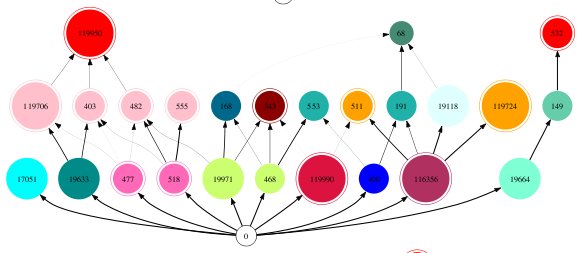When analysing output from the Webworld food web assembly algorithm (Drossel et al. 2001, J. Theor. Biol.), I often need a good way to quickly summarise the key properties of a web. In a recent project, I created a version of Webworld in which species could invade from outside the web (randomly generated species traits, as opposed to traits derived through mutation of a native species). I wanted to know what some of my food webs looked like, including information about their lineages, so started creating figures like the one below. Webworld food web diagram generated with dotty Species are...
Pretty food web graphs
When analysing output from the Webworld food web assembly algorithm (Drossel et al. 2001, J. Theor. Biol.), I often need a good way to quickly summarise the key properties of a web. In a recent project, I created a version of Webworld in which species could invade from outside the web (randomly generated species traits, as opposed to traits derived through mutation of a native species). I wanted to know what some of my food webs looked like, including information about their lineages, so started creating figures like the one below. Webworld food web diagram generated with dotty Species are...
Sep 3, 2010
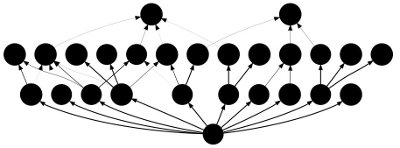A typical Webworld food web
I’ve finished up a draft module for Webworld (Drossel et al. 2001, J. Theor. Biol.) in Python that’s available for download: webworld.py
It’s also available bundled with what you’ll need for an example run: webworld.tar.gz.
Webworld for Python
A typical Webworld food web
I’ve finished up a draft module for Webworld (Drossel et al. 2001, J. Theor. Biol.) in Python that’s available for download: webworld.py
It’s also available bundled with what you’ll need for an example run: webworld.tar.gz.
Dec 31, 2008
A food web assembly algorithm is a series of repeating steps by which a model food web can be created. Starting with one or a few species, new species are permitted to invade at each time step, and are lost at each time step, according to some prespecified rules. There is already a large body of food web assembly literature (Tregonning & Roberts 1979, Post & Pimm 1983, Mithen & Lawton 1986, Taylor 1988, Drake 1990, Law & Blackford 1992, Luh & Pimm 1993, Law & Morton 1996, Lockwood et al. 1997, Drossel et al. 2001, Bastolla et al. 2005,...
Food web assembly algorithms
A food web assembly algorithm is a series of repeating steps by which a model food web can be created. Starting with one or a few species, new species are permitted to invade at each time step, and are lost at each time step, according to some prespecified rules. There is already a large body of food web assembly literature (Tregonning & Roberts 1979, Post & Pimm 1983, Mithen & Lawton 1986, Taylor 1988, Drake 1990, Law & Blackford 1992, Luh & Pimm 1993, Law & Morton 1996, Lockwood et al. 1997, Drossel et al. 2001, Bastolla et al. 2005,...
Nov 5, 2008
The change in the distance from the convex hull to the internal equilibrium during assembly
Law & Morton (unpub.) found that the distance between the interior equilibrium and the convex hull, measured as mean \(d\), increased as a permanent food web assembly progressed. I did a small set of assembly runs to test the robustness of this result, and to discover what causes \(d\) to increase. An introduction to permanence and example of how it is calculated can be found in a previous post. In verifying the result, I found that it was generally true for 2-prey, 2-predator webs regardless of the structure of the terminating web (Section 4.2). However it was not true for...Sep 5, 2008
Permanence and the distance from the convex hull to the interior equilibrium
Background To use permanence, Lotka-Volterra dynamics have to be assumed, because it is only in this case that a sufficient condition for permanence is known: \[\dot{x}_{i} = x_i \cdot f_i(x) = x_i \cdot (r_i + (A \cdot x)_i) \quad \forall i = 1, \ldots, n.\] Such a dynamical system is permanent if two conditions hold (Hofbauer and Sigmund 1988, The theory of evolution and dynamical systems p. 98). It is dissipative; this is true for Lotka-Volterra systems where all the basal species are self-limiting and heterotrophs cannot survive without their prey. That: \(P(x) = \prod_i x_{i}^{p_i}\) for some \(p_i>0\) is...May 4, 2006