Conservation managers often want us to predict how species will respond to different management options when we don’t have enough data to parameterise a dynamical model. Previously, we found that a popular Qualitative Modelling technique involving probabilistic analysis has philosophical problems and produces contradictory results. We proposed a new method, based on Boolean analysis, that remedied these problems (Kristensen et al. 2019 Meth Ecol Evol). However, it was still an open question how the Boolean approach would perform in a real-world application.

Yi Han’s new paper in Ecological Modelling is the first time the Boolean approach has been applied to a real-world problem. Christmas Island National Park, Australia, had been invaded by cats and rats. In 2015, an island-wide eradication of cats was initiated. However, there was concern that eradicating cats could release predation pressure on rats, who serve as both predators and prey for native species. We wanted to predict whether native species would respond positively or negatively to combined cat and rat control.

Figure 1: Yi Han consults with experts from Australian Parks and Christmas Island National Park <a href='https://buckleyecology.wordpress.com/2013/10/01/invasive-species-spaghetti-for-dinner-a-network-of-species-interactions-for-managing-invasive-cats-and-rats-on-christmas-island/#more-1943'>(Photo source)</a>
Figure 1: Yi Han consults with experts from Australian Parks and Christmas Island National Park (Photo source)

Yi compared the traditional probabilistic analysis with the new Boolean approach. When the probalistic approach was implemented in a mathematically correct way (see details in Appendix B), it was unable to determine whether a species would respond positively or negatively. The probabilistic approach assumes that, if a species response has a high probability in randomly parameterised models, then this provides high support for it occurring in the real world. However, if a species responds positively to cat control and negatively to rat control, or vice versa, then the overall response cannot be determined. Yi found that these undetermined responses were the most common prediction obtained from the probabilistic approach (striped regions in Fig. 2 below).

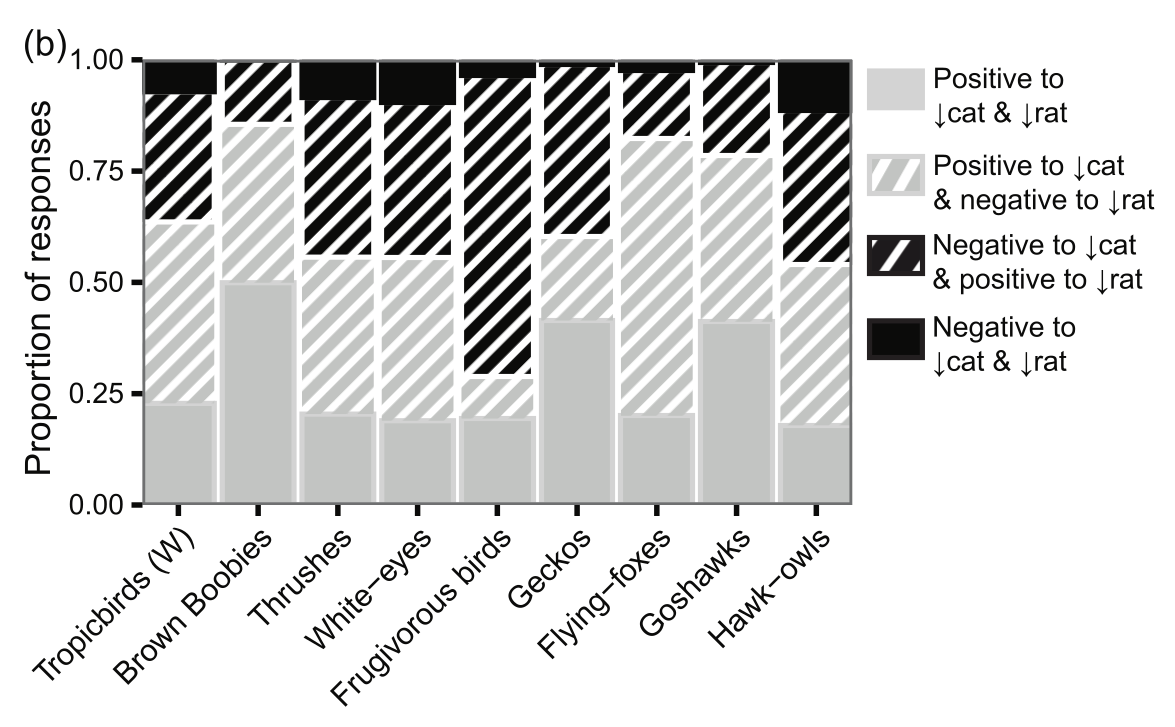
Figure 2: The probabilistic approach. Predictions of species responses to combined cat and rat management. The striped regions represent the proportion of models that could not determine whether the species' response would be positive or negative.
Figure 2: The probabilistic approach. Predictions of species responses to combined cat and rat management. The striped regions represent the proportion of models that could not determine whether the species' response would be positive or negative.

The Boolean-style solution to this problem is to ask the question in a contingent way. For example, we might ask, “If Species X responds positively to cat control, then will it respond positively or negatively to rat control?”. A preliminary Boolean analysis of cat control alone revealed the outcomes were contingent on the response of rats; in short, cat control only had guaranteed (in the model) positive outcomes if cat control also had a negative effect on rats (Fig. 3).

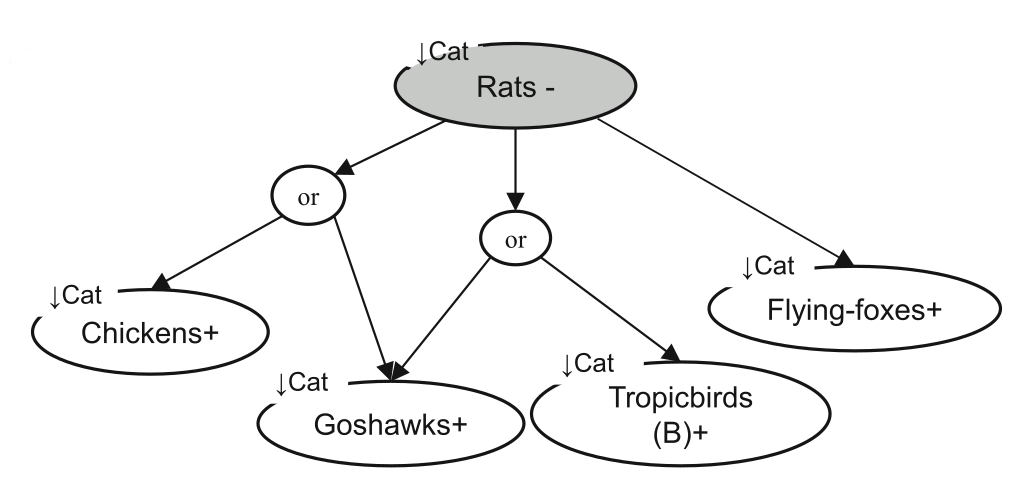
Figure 3: The Boolean approach. A summary of predicted species responses to cat control, where nodes and edges are to be read as logical implications. For example, 'If cat control has a negative effect on rats, then cat control will have a positive effect on tropicbirds or a positive effect on goshawks (or both)'.
Figure 3: The Boolean approach. A summary of predicted species responses to cat control, where nodes and edges are to be read as logical implications. For example, 'If cat control has a negative effect on rats, then cat control will have a positive effect on tropicbirds or a positive effect on goshawks (or both)'.

However, the most plausible scenario is that cat control will have a positive impact on rats, i.e. meso-predator release. When the model is premised on that scenario, then some predictions about the outcomes of combined cat and rat control can be obtained (Fig. 4). For example, the model predicts that, if cat control has a positive effect on the hawk-owl, then rat control will have a negative effect on them. This kind of result is useful because it tells us how to use a monitoring program. Hypothetically, if we observed an increase in hawk-owl populations in response to the cat control effort, then we would know to be cautious about subsequent rat control, and perhaps implement some additional programs to help support the hawk-owl population.

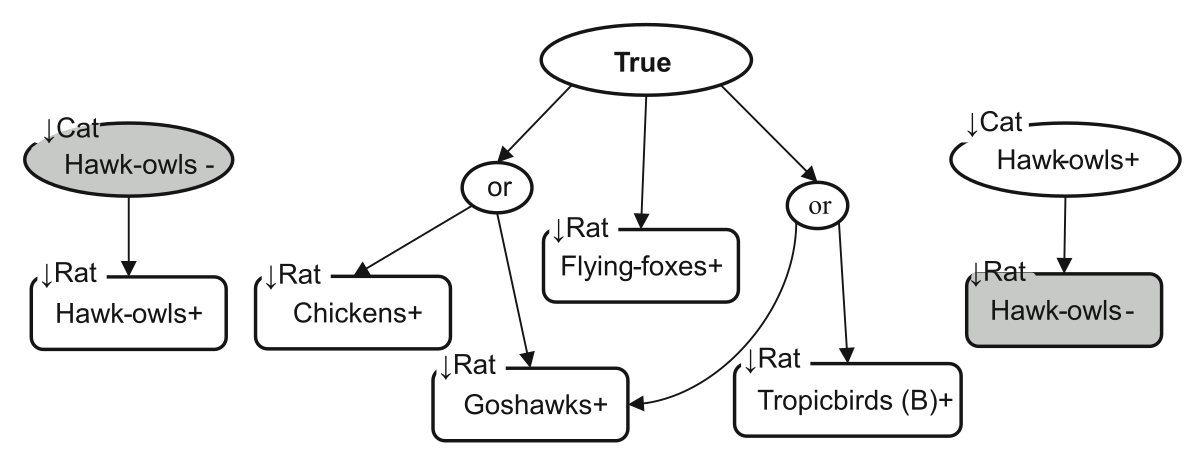
Figure 4: A summary of predicted species responses to both cat and rat control. The model is premised on cat control having a positive effect on rats, so logical implications should be interpreted contingent on that constraint. For example, the central edge from True reads: 'If cat control has a positive effect on rats, then rat control has a positive impact on flying foxes'.
Figure 4: A summary of predicted species responses to both cat and rat control. The model is premised on cat control having a positive effect on rats, so logical implications should be interpreted contingent on that constraint. For example, the central edge from True reads: 'If cat control has a positive effect on rats, then rat control has a positive impact on flying foxes'.

The paper discusses some other pros and cons of the Boolean approach that were encountered in the study. One practical downside is that it is more challenging to use. It is conceptually more difficult, e.g. one needs to become comfortable with formal logic and Boolean algebra, and it is also more difficult to code. To remedy this, Yi has done a fantastic job of converting my Python implementation into R, and written a tutorial for how to use the code (in Appendix C of the paper). We hope that this will make the work more accessible for others.

References:

Han, Y., Kristensen, N.P., Buckley, Y.M., Maple, D.J., West, J., McDonald-Madden, E. (2020) Predicting the ecosystem-wide impacts of eradication with limited information using a qualitative modelling approach, Ecological Modelling, 430:109122, (Github), (pdf)

Kristensen, N.P., Chisholm, R.A., McDonald-Madden, E. (2019) Dealing with high uncertainty in qualitative network models using Boolean analysis, Methods in Ecology and Evolution, 10: 1048-1061, (pdf), (Github)