New solutions for Parker sperm competition model
Parker et al. (2013) created a general model for sperm allocation under a trade-off between male investment of resources \(R\) into pre-copulatory effort (e.g. search time) \(T\) versus post-copulatory effort (e.g. ejaculate) \(U\). Their model is interesting because it encompasses a range of different scenarios of female remating and the type of competition between males. For female remating scenarios, the risk model has females mating a second time with probability \(q\), with the possibility that being first or second leads to higher fertilisation rate (`loaded raffles’); whereas the intensity model has females mating with \(N > 2\) males on average. For male competition scenarios, scramble competition has every male competing for every mating opportunity (\(M \rightarrow \infty\)); alternatively, groups of \(M\) males may compete per mating opportunity. The average number of matings \(n\) that a mutant male achieves was given a nice flexible functional form (their Eq. 6), so that the shape of the relationship between a mutant’s relative number of matings versus pre-copulatory expenditure (their Fig. 1) could be controlled by a parameter \(a\).
Parker et al. (2013) used these models to obtain the ESS for the units of sperm per ejaculate, \(s\). They were able to solve the ESS analytically for the following scenarios: \(a=1\), implying that males gain matings with increased pre-copulatory expenditure in a linear way; and \(M \rightarrow \infty\), implying scramble competition. For other scenarios, there was no analytical solution, basically because the flexible form they gave \(n\).
Out of curiosity, I rewrote their model so that the pre-copulatory effort \(T\) was treated as the trait under selection. I found that, by doing so, I was able to get analytic solutions for three of their four scenarios for the full \(a\) and \(M\) parameter range, and a semi-analytic solution for the remaining scenario. Python code to reproduce my results can be found on Github.
When \(T\) is the trait space, their Eq. 6 (the number of matings the mutant male obtains) can be left as it is:
\[n(M,T,\hat{T}) = M \hat{n} \left( \frac{T^a}{T^a + (M-1)\hat{T}^a} \right).\]This avoids the complication introduced by having \(n\) in terms of \(s\) in their Eq. 9. Then the derivative \(d n(M,T,\hat{T}) / dT\) can be obtained straightforwardly.
To use \(T\) as the trait space, the expressions for the value for each mating, \(v(s,\hat{s})\), must be converted into \(v(T,\hat{T})\). The conversion is obtained by using their Eq. 3a
\[s = \frac{R - T} {n(T,\hat{T})D},\]and
\[\hat{s} = \frac{R - \hat{T}} {\hat{n}},\]They give the expression for fitness
\[w(T, \hat{T}) = n(T, \hat{T}) \: v(T, \hat{T}).\]Then the singular strategies can be found by solving for \(T^*\) such that
\[\left. \frac{d w(T,\hat{T})}{dT} \right|_{T = \hat{T} = T^*} = 0\]For the intensity model, I found two singular strategies, \(T^*=R\), and
\[T_{I}^* = \frac{ {\left(M - 1\right)} R a}{ {\left(M - 1\right)} a + M \hat{n} - M}\]For \(M \rightarrow \infty\) (taking limit of above)
\(T_{I}^* = \frac{ R a}{ a + \hat{n} - 1}\)
For the risk model, a general analytic expression for \(T^*\) cannot be found. Instead, a semi-analytic solution is found, where the roots of an equation must be solved with a numerical root-finding algorithm. (I haven’t included the equation here because it’s a bit long, but you’ll find it in the code).
For \(M \rightarrow \infty\), two singular strategies are obtained, \(T^*=R\), and
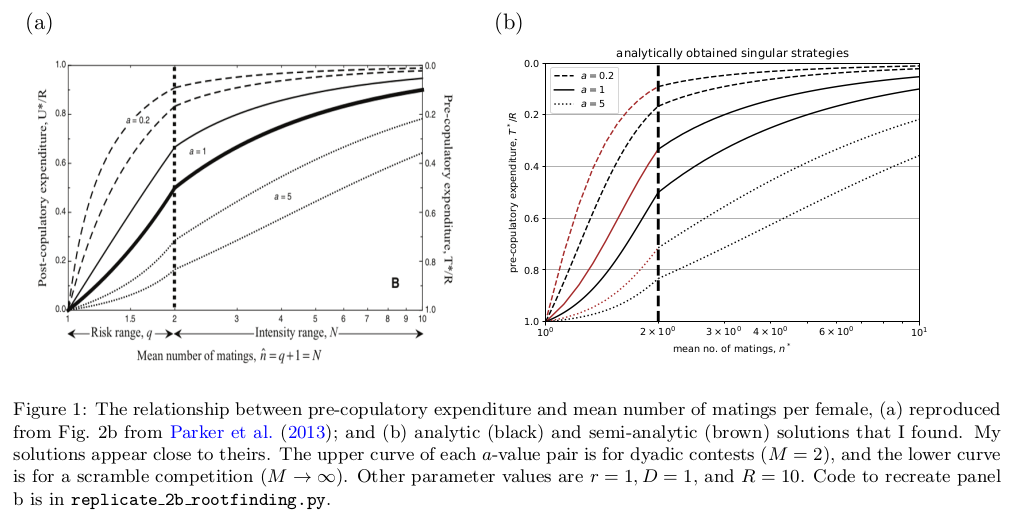
\[T_{R}^* = \frac{ {\left({\left(\hat{n}^{2} - 3 \, \hat{n} + 3\right)} r^{2} - 2 \, {\left(\hat{n} - 2\right)} r + 1\right)} R a}{ {\left(a \hat{n}^{2} - 3 \, a \hat{n} + 3 \, a\right)} r^{2} - {\left({\left(2 \, a + 1\right)} \hat{n} - \hat{n}^{2} - 4 \, a\right)} r + a}.\]To check that my solutions above were correct, I tried to replicate their Fig. 2b. My solutions appear to be pretty close their results.
Reference:
Parker, G. A., Lessells, C. M. and Simmons, L. W. (2013). Sperm competition games: a general model for precopulatory male–male competition, Evolution 67(1): 95–109.