Law & Morton (unpub.) found that the distance between the interior equilibrium and the convex hull, measured as mean \(d\), increased as a permanent food web assembly progressed. I did a small set of assembly runs to test the robustness of this result, and to discover what causes \(d\) to increase.

An introduction to permanence and example of how it is calculated can be found in a previous post.

In verifying the result, I found that it was generally true for 2-prey, 2-predator webs regardless of the structure of the terminating web (Section 4.2). However it was not true for other 3-species and 4-species web structures for which d tended to decreases as the assembly.

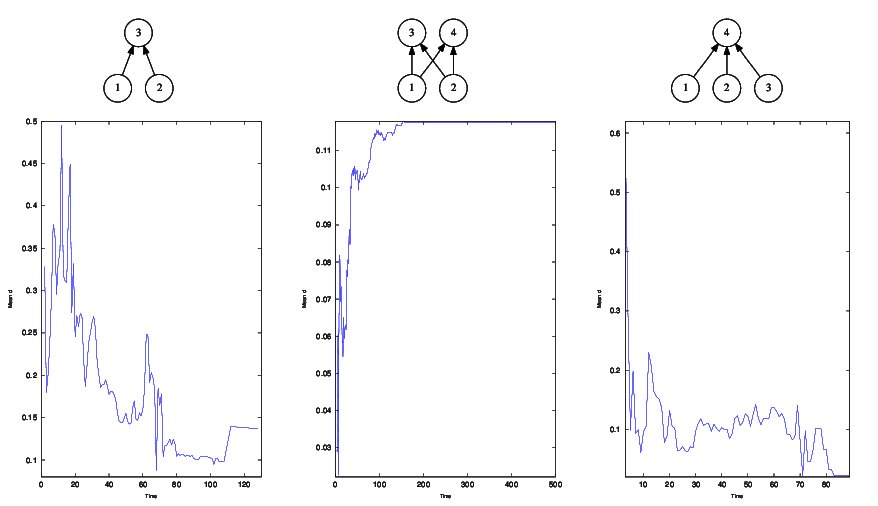
Value of d as the assembly progressed
Value of d as the assembly progressed

In all of the structures investigated, the replacement of a basal species tended to increase \(d\) and the replacement of a consumer species tended to decrease it.

When the species replaced is basal, the internal equilibrium tends to move further away from the origin, leading to the increase in \(d\). However when it is a consumer, the internal equilibrium tends to move closer to the origin, and the height of the hyperplane tends to increase, which leads to the decrease in \(d\).

The movement of the internal equilibrium away from the origin when the replaced species is basal is partially explained by the change in biomass of the species that is replaced.If the replaced species is basal, the successful invader tends to have a higher steady-state biomass in the full system, and if the species is a consumer it tends to decrease.