Thinking about this problem, I started thinking about point-and-click adventure games– they are good at facilitating productive struggle. They let you try and fail, and they nudge you forward without handing the answer to you. They make you want to persist. I wondered if we could do something like that.

This semester, I built two interactive linear algebra worksheets for MXB106: two weeks, two multipart questions. I embedded them into Canvas, the learning management system used at QUT. You can visit them here: Week 8, Week 9.

The key design feature was branching paths: the student chooses their level of scaffolding and decides where to go next.

Hints are nested, to reveal gradually, so students retain the satisfaction of solving the problem.

And when the student gets the answer wrong, the response isn’t “Wrong, try again”, it’s “We’re going to learn this together”, e.g., with a step-by-step guide.

I also collected detailed anonymised tracking data — I know exactly which path each student took, where they clicked, and when — so I could watch exactly how it worked.

Remember my main goal was to reach students who are unable to attend in-person workshops. As luck would have it, in the second week of the trial, the Monday workshop was cancelled due to ANZAC Day– and that’s where he had our second-largest spike of activity. When students couldn’t get to their workshop, they used the interactive online version instead.

With the detailed tracking data, I was able to focus in on students who fully engaged with the worksheets and worked outside workshop hours. In the first week, 40% worked outside workshop hours; in the second week, 85% did.

I could also see the hours when they were working. We had some students doing linear algebra at 1 am in the morning.

When I tightened the data again to look at those working exclusively outside workshop hours and deeply engaged, I estimate we picked up about 45 students, which is equivalent to about 2 or 3 in-person workshops.

But did it work?

For this pilot trial, we had selected questions from the existing worksheets that addressed the upcoming assignment in some way. Compared to previous years, marks improved on every question (all statistically significant, BH p < 0.03) with an overall improvement of 12 percentage points.

We also had some positive qualitative feedback. One student emailed to request more worksheets, and the in-person feedback was positive as well.

So it seems the online worksheets not only improved marks, students also found them valuable.

Further reading

I presented talk today at the Faculty Learning & Teaching Colloquium about the worksheets. A link to the presentation slides is here.

The Unit Coordinator is transforming the MXB261 into a game theory unit, and the first 7 weeks were “old” material she will replace in the coming years. Students responded really well to the new game theory content, describing it in the survey as “fascinating” and “mind blowing”.

Nonetheless, the old material was also quite interesting; one student still wanted to “go down the ODE rabbit hole” after the exam. The unit had no maths prerequisites, so any second- or third-year student curious about modelling could join, and it offered a “taster” of different modelling techniques, including Monte Carlo simulation, Markov processes, and ODE models. The case studies were focused on ecological applications, and it attracted students from maths, data science, and environmental science. I think it was quite unique with its goal of broadening students’ knowledge rather than going deep on a particular topic, and I would have really enjoyed it as a second-year undergrad (I did environmental engineering). I hope that the students will draw on it later in their professional career; if they have a particular problem to solve, I hope they will remember which types of techniques can be used to solve it, and build from the basic principles they learned here to teach themselves the rest of what they need to know.

The interactive lectures were “hybrid” lectures with students attending both in-person and online. The first half was typically structured more like a traditional lecture but with active-learning opportunities. I would work through additional material and the self-study activity, but pepper it with Q&A and pair-and-share. The second half was space for students to ask questions and get help with their assignments.

One challenge was teaching to students from a range of backgrounds. Some students found the MATLAB coding trivial but were thrown by mathematical notation, while others felt at ease with the mathematics but struggled with coding. So before each interactive lecture, I would review the activity and workshops, watch the online recorded lecture, and think about my 2 imaginary students: one who is good at maths but struggles with coding, and another who is comfortable with coding but not with maths. What is the implicitly assumed knowledge they might not have? What would they find unfamiliar and difficult? That would guide my content for the interactive lecture.

Below, I will share the first half of one lecture I gave. For this lecture, I noticed that the online recordings assumed that students would be familiar with initial-value problems and stability. For example, the stability conditions were given without an explanation for why they were so. So my lecture introduces quiver plots as a visual tool for understanding ODEs, then uses them to build intuition for steady states and stability, before moving to cobweb plots to explain numerical stability in Euler’s method.

It took quite a while to prepare this lecture, so perhaps this will save someone some time. The full list of MATLAB scripts used to create the figures is available from this blog’s repository, and I’ll link them in context below. One thing I found really helpful was to plot a thin grey line where I intended to draw during the lecture. The lines aren’t visible on the slides below, but were visible on the tablet I used, and that’s much safer than trying to free-hand it.

Although it might embarrass me a little, I’ve decided not to edit out my verbal hiccups. The transcript is pretty much how Zoom transcribed it except I removed some exchanges I had with students, added ellipses and removed muttering when I pause to draw, and corrected some Zoom-transcription errors. I’ve benefitted from looking at the transcripts of others’ lectures and seeing those verbal imperfections. The transcript also helped me notice a few verbal tics I would like to correct. I have almost succeeded in removing “um” and “like” from my vocabulary, but it’s a journey. I think I could reduce the number of sentences I start with “So…”. The main thing I would like to correct is my use of gendered language (“you guys”). This is not a good habit, particularly when I’m teaching maths.

Lecture transcript

In your online lectures, you looked at deterministic population growth models, unconstrained growth, constrained growth. Then you looked at Euler’s method, and then a little bit of cool stuff with period doubling and chaos.

So, there’s no prerequisites for this course, and I know that, if that was the first time I’d seen this kind of thing, I would have been pretty bewildered. There’s certainly a lot of guidance on how to use Euler’s method and stuff like that, but learning is more than doing the activity, it’s understanding the meaning behind it. And so what I thought I’d do for this interactive lecture is introduce you to some visual tools to help you understand what’s really going on behind this maths.

So for those of you whose expertise is in coding and not so much in maths, I hope that this will be useful for you.

So it’s actually a legal requirement that any lecturer who talks about stability has to use the balls on a hill analogy. So, I’m going to do that. I’m going to consider two balls on a landscape. I’ll give this one an open circle, and this one a closed circle, and this is an analogy for the concept of steady state and stability.

In this, analogy, the ball position is like a system state. So we could imagine that the position here is Y, for instance, and gravity provides us our system dynamics. Now, these two balls, one perched on the hill and one in the valley, are both at steady state. So the meaning of steady state is that something doesn’t change with time. And both of these balls, as we watch them … they’re not moving.

But there is a sense that one of these balls is more stable than the other. Intuitively, a stable steady state would be the example of the ball at the bottom of the hill, that if we give it a small perturbation, if I pushed to the left, it would roll back to where it was. Whereas an unstable steady state is the ball at the top of the hill, where if I give it a bit of a push, then it’ll roll off down the hill and go away from that steady state that it started at.

So in your online lectures, this question of stability was discussed in the context of two distinct aspects of the population growth modelling that you were looking at. What were those aspects? I’m going to get you to pair-and-share. And I am going to try something exciting and create a breakout room for the people online so that you can discuss as well, so hold on to your socks.

(Pair-and-share. No one was able to answer)

Fair enough. Okay, well, this is a great lecture, because I’m going to show you exactly what those two aspects of stability were. So I’ll just write them here… The two aspects of stability were the dynamics of the model itself. So the stability of the population. And the other aspect of stability was the stability of the numerical solution to the dynamics. So, in this lecture, I want to introduce some kind of visual tools to help us get a handle on these two aspects of stability.

We’re given a class of problems called the initial value problem. And so the idea is that you’re given some kind of differential equation. These equations describe how the state variables change over time. So, in this case, the population size changes over time. And we’re interested in finding the trajectory of the population given the initial population size, given the initial values. And so, in this case, we start with Y at T equals 0 equals YO, and in the online slides, you are given these solutions to YT.

But I think maybe it might not have been so clear where these solutions came from. Certainly these examples have analytic solutions, but when we’re modelling– I mean, if we’ve got an analytic solution, we’re not going to break out the MATLAB, right? We just write it on a piece of paper. And so usually, when you’re using these sorts of techniques, you don’t have an analytic solution. And it’s not super obvious where these solutions came from.

So, what I want to do is first introduce you a tool called the quiver plot. And this is a visual tool for understanding how the system dynamics works.

Figure scripts: plot_one_quiver.m

So, in this case, I’m going to look at the unconstrained growth, model. So dY dT equals lambda y, and I’ve just set lambda equal to 0.3. So the idea of the quiver plot is that we, say, start at a point, say y equals 3, T equals 2, What we’re going to do is we’re going to take a delta T. In this case, I’ll set delta T to 1. And then we calculate, with that delta T, what will be our delta Y? So, we calculate our delta Y, is equal to 0.3 Y delta T. And so that would be, in this case, 0.3 times 3 times 1, because I set this one to 1. And so that’s how we get the length of this arrow here.

And then we basically draw an arrow in space, like that, on our graph. So here was Y equals 3, T equals 2, so that’s that point. And so, if I move along in time by one step, then I go up by … sorry, I forgot to do the final calculation … 0.9. Then we move up by 0.9, so up to there, so we draw a little arrow like this.

And so we can do that at various points in the grid. For example, let’s start here with Y equals 6, T equals 4. So we’re gonna take a step of T equals 1, and so the height of Y will be, let’s see, 6 times 0.3 is 1.8, so we’ve got to go to there. So we draw an arrow like that.

And we can do this in every spot on our grid to get a kind of sense of the dynamics… This is an important one. When Y equals zero, always the change in Y will be equal to 0.

And so imagine that I did this for the entire space of Y versus T. And I end up with this plot, which is called the quiver plot.

Figure scripts: plot_expon_growth.m

And this is fantastic, because this is DYDT equals lambda y. These little arrows are like a visual representation of the differential equation that you can see with your human eyeballs.

In addition, it has this very intuitive feeling about it, like there’s a flow of Y in time. And that intuition is correct. We can basically use that flow to understand where our solutions to DYDT equals lambda y goes from various initial values.

So let me be concrete about that. Let’s say I want to start at Y0 equals 1. So I put a little dot here. Now, you can see that there’s an arrow in that direction, and so I’m going to draw a line in that direction. This is Y changing with time. As Y gets larger, it gets entrained into these arrows that are headed more upwards. And so it increases … at an increasing rate … like this. And so that’s it, that’s one solution to the initial value problem, YO equals 1.

We can do another one. Let’s say we want to start at YO equals 2 … we catch our arrow, and we follow those arrows through time.

Here’s YO equals 4.

And of course, a pretty important one, Y equals zero … Our arrows are just going along like this, through time.

And so that’s how the initial value problem works, that dy dt gives us this … well, there’s an infinite number of arrows, but I can only draw so many. The initial value gives us where our solution starts, and the differential equation how we’re going to follow that flow through time.

Figure scripts: plot_expon_decline.m

So that was the unconstrained growth model. Here’s another example with population decay. So this is the quiver plot, but it’s pointing in the other direction now, because our lambda is a negative number here. And we can do the same thing again.

So let’s start at YO equals 10, and we’re following our arrows down… And that’s one of our solutions to the problem.

If Y equals 4, start at 4, Following it down … And that’s another way that the population might change over time. Here’s another one. And if we have zero … then they will stay zero forever.

Figure scripts: plot_logistic.m

This one is the dynamics of the constrained growth, and it’s a bit more exciting because we’ve got arrows going in different directions, but the same principle applies. So we start at YO equals 0 … If we have no animals, there’ll be none forever.

Y equals 2 …

This is a special value: this is 8, the carrying capacity. And so if we’re at carrying capacity, we stay at carrying capacity forever.

And if we’re above it, well, that’s too many, so some … some animals are going to die… it’s the generations turn over, and we’ll go back down to carrying capacity.

So that’s where those lines came from in the online lectures. You can solve them analytically, but in the cases where you cannot, this is a kind of visual understanding of where the solution comes from.

Figure scripts: plot_expon_growth_compact.m

So, remember, our analogy of the balls? We’ve got the unstable ball here … The stable ball here.

The first question we ask ourselves is, well, in the analogy, both of the balls were at steady state, because if we watch them through time, they don’t change.

And so, is there some point in this, in this flow, where if Y is at that value, it doesn’t change through time? And so, we’re looking at this, and … evidently, if we start at zero … we stay at zero forever. And so we will call this our steady state. Indicate it with a star … equals zero.

Now, the next question, is it stable or unstable?

So, when we’re thinking about our balls, if we give them a bit of a push, do they come back to where they were, or do they roll off to somewhere else?

So let’s give our steady state a bit of a push… And it gets entrained by an arrow that’s ever so slightly going upwards. And then it rolls away from y equals 0. So that means that Y star equals 0 is unstable.

Figure scripts: plot_expon_growth_compact.m, plot_expon_decline_compact.m, plot_logistic_compact.m

So I just did the unconstrained growth example, and I think that, as a pair-and-share, you guys could do the other three cases.

So do the population decay and do the constrained growth, identify the steady states first, and then mark them unstable or stable. Alright, I’m gonna try this breakout rooms thing again.

(Pair-and-share)

Okay, yeah, so, so what did we conclude for the population decay one? What’s the steady state for that one? Plug it into the chat or shout out. Y is 0. Yeah, awesome, yes, exactly!

So in Y-Star, Equals zero, that’s our steady state. And is this one stable or unstable? Will be stable? Chat? You didn’t hear that answer, so have you guys got an answer to whether it’s stable or unstable? Stable, awesome, yeah! So you’ve got the idea that if you give this a bit of a push. Then it’s going to come back to where it was before.

Okay, now this one’s a bit more complicated. It’s got two steady states. Let’s just pick one. What’s one of the steady states? That’s the full answer from the chat! Real fast. Yes, excellent. So here’s a … steady state, Y star equals 0. And this one is unstable, because if we give it a bit of a push, it’ll get entrained into those, arrows and move away. And then there’s Y star equals H, which was our carrying capacity, and this one’s stable. And so you can see that if we push it up or down, it’s going to come back to where it was before.

Alright, so we’ve got our intuition nice and primed!

But we’re probably not going to be plotting quiver plots to understand the stability of our system. So, is there some kind of mathematical way that we can capture this intuition and do it with maths?

Figure scripts: plot_logistic_compact.m

So, steady state means that there’s no change in time. And so that means that we’re looking for a DYDT that stays zero for the, entire time.

So I’ve got a bit of new notation here that might be new to you. What this means is it’s “evaluated at”. So I’m going to calculate DYDT, but I’m going to evaluate it at the particular Y star that it will be equal to 0 at.

That was a bit of a clunky explanation. Your online lecturer uses FY star equals 0 instead… I find F not very descriptive, so I’m going to keep using this notation here.

So let me give you a concrete example. Here’s the constrained growth. There’s my DYDT. And so what I do is I substitute in everywhere where there’s a Y, I’m going to put in a Y star. And I’m going to make that equal to zero, and then I’m going to try to solve it.

What are the Y stars that make this equal to zero? So, we’ve got a product here, so that means that it can be zero if either this part is equal to zero, or that part is equal to zero. So this left-hand side, that’s equal to zero when y star itself is equal to zero, so that’s that solution there. And this right-hand side, well, that would be equal to 0 if Y star on 8 is equal to 1, which means that Y star is equal to 8, and so that’s… So that’s how we get our steady states mathematically.

Okay, so we’ve got our steady states. But how can we tell if they’re stable or unstable? We’ve been looking at the quiver plot so far, but is there some mathematical way to check if it’s stable or unstable as well?

And so, in your online lectures, you’re given, in particular, this part here is the important bit. So apparently, if this derivative is less than zero, then it’s stable.

Okay, cool. So we could memorize that, but why is that the case? Like, can we get some intuition going for this?

Figure scripts: plot_expon_growth_compact.m, plot_expon_growth_dydt.m

So, to get the intuition for this, I’m going to do something, a little bit new. This is the plot that I had before. Here, DYDT versus Y. And so I’m looking at my unconstrained growth again.

And this is the line that I’m interested in plotting… DYDT versus Y.

When y equals 0, DYDT equals 0, so we’ll start here. And what’s an easy second point? When y equals 10, DYDT equals 3, so we’re going to that point there. So this is a straight line. So that’s our DYDT versus Y.

So now, what I’m going to do is I’m going to draw a cartoon of the dynamics on this axis here. And, this is something that’s commonly done in the literature, I’m going to use the same conventions as them.

So, what I’m going to do is, on this axis, on this line, I’m going to draw an arrow that goes in the positive direction, if there’s a positive change. If DYDT has, if Y has a positive change, or DYDT is positive. And I’m going to draw an arrow going in the negative direction, if it’s negative.

And I’m also going to identify the steady states by drawing an open circle … for our unstable states, and a closed circle … for our stable states. So it’s the same as the balls before. I planned ahead.

Alright, so how do we do this? So, I’m looking at DYDT, and I see that it’s positive, so I’m going to draw an arrow like this.

I could go a little bit further. I know that then when Y is quite large, the arrow is quite large. But then Y is small, the arrow is small. And indeed, DYDT here is high when it’s high and low when it’s low. So I could draw a … big arrow here, and a small arrow here, to kind of indicate that.

And so I know that the steady state is where Y equals 0, and at this point, I can actually just stop thinking and look at where the arrows are pointing. The arrows are pointing away from the steady state. So that means there’s an unstable steady state. So I’m going to put an open circle right here.

So this is my cartoon for the dynamics.

Figure scripts: plot_expon_decline_compact.m, plot_expon_decline_dydt.m

Do the same thing for the population decay. So, we’re going to draw a… DYDT on this axis, and Y on that axis. So when Y is 0, that equals 0. This time it’s a negative 3 with y equals 10. And I see that everywhere … this is negative, so I’m going to draw the negative arrow. And so the arrow is pointing towards my steady state, and so I’m going to put a stable steady state there.

Figure scripts: plot_logistic_compact.m, plot_logistic_dydt.m

This is the fun one. So this, DYDT, it ends up being a bit of a curve … that starts here … and then goes down like this.

I think the purpose of all of these sorts of things is to not have to think too hard. So what have we got? We’ve got positive here … in here, it’s negative. And so immediately, I’ve got it: unstable steady-state, stable steady-state.

Figure scripts: plot_expon_growth_compact.m, plot_expon_decline_compact.m, plot_logistic_compact.m, plot_expon_growth_stability.m, plot_expon_decline_stability.m, plot_logistic_stability.m

Alright, so these are the examples together. This one had an arrow going that way, that one had an arrow going that way … this one has arrow going like this. And in fact, I could have drawn the arrows first, and then decided on the stability.

Are there any questions about that so far?

At this point, we’re just kind of creating a visual tool, and it’s going to hopefully get us towards the maths in a moment.

No questions from chat? Okay, we’ll keep going.

Figure scripts: plot_expon_growth_stability.m, plot_expon_decline_stability.m, plot_logistic_stability.m

Alright, so those were my examples that I just went through before. And so what I’m going to do is I’m going to get you to all pair and share. I’ve given you an arbitrary DYDT versus Y curve here, and I want you to do the same thing that I did before. Find out where the arrows point, and then find out where the steady and the stable and unstable steady states are. We’re gonna do the breakout rooms again. Getting good at this.

(Pair and share)

Alright, so .. help me out here while I do it. So, okay, let’s start at this point. Am I drawing a positive or negative arrow at that point? I hear a whisper of positive. Heading right, yes. Okay, and how about this one here, in between? Left! Alright, I think you guys get it. And so, this one’s positive because the curve is above, and it’s positive, and this one’s negative because it’s above it.

And so at this point, we don’t have to think anymore. This one’s stable, this one’s unstable, this one’s stable, this one’s unstable, this one’s stable.

Alright, now there was a second part: what is it that distinguishes the stable from the unstable steady states? With respect to the slope of the blue curve at those steady states? Did anyone notice a pattern?

Hmm. Over to under means stable, and under to over means unstable. Yep, definitely. So, yes. Over to under means stable. So, over to under.

What would the slope of that be? Would that be positive or negative? Yeah, you got it. It is, it’s negative. So this one’s got a negative slope. And this one’s got a positive slope.

I’m talking about the slope of the blue line, right? At this point, the blue line has a negative slope. At this point, it has a positive slope. At this point, it has a negative slope.

So it looks to us that the thing that distinguishes our stable from our unstable steady states is the slope of dydt with respect to Y.

Okay, so let’s consolidate all that. When we’ve got a positive slope, it’s unstable. When we’ve got a negative slope, it’s stable. So how could we write this mathematically?

So, we’ve got DYDT on this axis, and Y on that axis. So, slope is d-something d-something, and it’s DY on the bottom because that’s the one that’s on our x-axis, as confusing as that is.

And what is it the slope of? Well, it’s the slope of DYDT. So this is the … this is the quantity that we’re using to determine whether our steady state is stable or unstable.

Now, this function will give us the value of that slope at every point. But we’re not interested in, like, the slope here, or here. We want it specifically at the steady states, right? So then we’re going to use our line notation to say we’re going to evaluate that … at Y equals Y star. So this is one of our Y stars, for instance. So this here … means evaluated here.

So I’ve written that out here, each of the cases. We’ve got a stable steady state when the slope of DYDT with respect to Y evaluated at Y star is negative. In your online lecture notes, they used a more abbreviated notation … like this … where it’s understood that F is DYDT, but I find that kind of counterintuitive. I like it to be more verbose, so I know what’s going on.

And likewise, if it’s an unstable steady state, well, we’re looking at that same quantity, but it has to be positive. And so, in your lecture notes, it looks like that. And so, you know what? Now you understand what that online lecture was saying.

(Student asks: What if the derivative is zero?)

You want to know about the equals zero case, don’t you? Okay, let’s do it. Alright, so let’s imagine… well, let’s look at an example. So, if we had … DYDT, and we had Y, in order to have it exactly zero, we’re going to need something like this … at our Y star, it has to be flat. And so one way we could do that is we could have it … looking like this. So what would that look like in our quiver plot? Let’s say that, I put my Y star here, and this is time. So now I’m doing Y versus T. So it means that as we’re approaching Y-STAR … our, our, … well, let’s see, they were, they were quite … and then they kind of went like this … and then they went like that, and then they went like that. But then they go positive again instead of going negative, and so they go up like that. So, if you imagine that one trajectory as a huge quiver plot — I’ll draw a better picture of this for the annotated notes — then that would be what you’re looking at, so it’s a point of inflection. … All of the examples you’ll be working through, it’s either positive or negative, so you don’t look at this kind of this in-between-y situation.

Are there any more questions about that? How about you, chat? I’m looking at the window. It’s all good. Alright.

Okay, so now we’ve got a mathematical way to do this, let’s do an example, a concrete example, so we can really solidify this.

Figure scripts: plot_logistic_stability.m

So, this is our constrained growth again, because it’s my favourite. And we’ve got the dynamics here, and these steady states we found before. They were Y equals 0 and Y equals… Y star equals 8. And we knew from drawing our picture when it was unstable or stable, but let’s do it with maths to verify.

So, we want to look for, it’s stable if DDY of DYDT, evaluated at Y star is less than 0. So the first thing I do is, I just rearranged it, I expanded it out, because it’s easier to take the derivative then. So, I want to take the derivative of Y on 2, so that’s 1 on 2, so that’s that first term there. And this turns into 2Y on 16, which is Y on 8, so that’s there, and there’s your negative coming over. And so, at this step, now we need to — because we don’t want to know about the slope there, we want to know about it here and here, at each of the steady states — so we’re going to look at each of the steady states.

When Y star equals zero, what we do is we substitute Y equals 0 into this, so that would make this part 0, and that would leave a half, so that’s our half there. Half is greater than zero, so it’s unstable, which is something we verified before.

Now let’s think about when Y star equals 8. So if we put an 8 in here, that’s a 1, and a half minus 1 is a negative half, and so that’s that negative half there. Negative half is less than 0, and so it’s stable, and we knew that from before. Are there any questions about that?

Cool. So that was one aspect that stability that is important to us in population modelling, the stability of the dynamics of the model itself, of the population itself, at its different points in Y.

The second aspect is the stability of the numerical solution to the model. And so there’s similar concepts, but subtly different concepts here, and it can get a bit confusing.

In your online lectures– I am going to abbreviate the notation now, I’m going to write F of Y for DYDT – and you would be given an initial value, YO, and you’re given a constant step size and time, which is H, and then you can just kind of churn through the maths. What you do is you get your YO … you put it into this equation and in here to calculate your Y1. And then you substitute your Y1 in to get your Y2, and yada yada yada. And it’s really boring. But what’s actually going on behind here? Something exciting.

Figure scripts: plot_expon_growth_euler.m

Let’s take a concrete example, using, again, this awesome tool called Quiverplot. So … Here I am using my abbreviated notation for this particular example. I’m going to start at Y equals 1, and we know that our analytic solution here is this curve. So I’m going to take a step size of H equals 5. So what I’m saying is that I’m going to step forward in time by 5. So, just to make that … clear, I’m going to put a dotted line at the 5 … and at the 10 … That’s what we’re heading towards.

Alright, so you have seen examples of how to do this mathematically, here, we have the first two steps. So get Y0 equals 1 … we substitute it in, so there’s our 1. This here is our 5 from the H. 0.3 is that 0.3 up there. 1 is because we’re at H … YO equals 1 … and that equals 2.5. And then we can substitute that in to get the next one. So we put 2.5 in here and in here. This part here is the DYDT, and we get 6.25.

It doesn’t feel very meaningful. But we can understand what’s going on if we draw what the Euler method is doing visually.

So when we’re at YO, we’re starting here. And we’re going to take a step to calculate our Y1. What we’re doing is we’re catching this arrow that’s pointing in this direction. What we’re going to do is we’re going to say that’s the derivative of this function until we hit the wall at 5, so we’re going to project ourselves forward…. And here we are … that’s our Y1 at 2.5.

That’s what the Euler Method does. It takes the derivative at the point you started at, and steps forward in time using that derivative to get the next value.

At this point here, we’ve got an arrow that kind of points in that direction. And so we’re going to assume that that’s constant until our next point in time. And so we get to this point here … and so if I’ve drawn it well, that should be 6.25.

You can imagine that if I took more sensibly small steps, I would have tracked the value a little closer. But I took these big steps, because I wanted to show you the first issue with Euler’s method, which is that it’s not so great. So you can see here … Take the distance from, say, here to here … this is a lot of error. And you can imagine, as this red line goes up, the error’s just getting worse and worse. That’s also true if I’d have taken smaller step sizes, that error would be getting worse and worse, but it’s easier to draw them large.

So you might be thinking, well, maybe that’s just because this is, like, the exponential growth, and so maybe if you had some true … solution that sort of asymptotes that you would kind of … the solution that you’re finding with Euler’s method will get closer and closer to the true value. And that’s true, that is good intuition, and that is correct.

However, there’s other perverse things that can happen with the Euler’s method, even when you’ve got this asymptoting kind of situation. And so that brings us to the second aspect of stability, which is not the stability of the dynamics themselves, but the stability of the Euler method, whether it converges on the steady state of the dynamics or not.

So let me make that concrete.

Figure scripts: plot_logistic_euler.m

So, here I’m taking really small step sizes … H equals 1 … And there’s my first step, my second step, my third step. The reason I’m able to do this is because I put a grey line in there to help myself later. And you can see it nicely converges to the dynamical, stable steady state. So the numerical solution is smoothly converging to the steady state, and here we would say that the numerical solution is stable.

Figure scripts: plot_logistic_euler.m

Let’s take slightly bigger step sizes. I’m going to use a step size of 3.5 this time. So my first step takes me to here … My next step takes me to here … The next step takes me to here, oh, wow, I bumped over the steady-state. … then I bumped back … Boom, up, and down … But each bump, I’m getting closer and closer, until the bumps are kind of hard to see, and it basically looks like …

So, this numerical solution also converges to the dynamical steady state, but it does it in this oscillatory way. It goes above and below and above and below, switching, until … but it’s getting closer and closer. So we can say the numerical solution is also stable in this situation.

Figure scripts: plot_logistic_euler.m

Let’s make our step size even bigger. Alright, 4.5. So, take a step of 4.5, up to here … The next step gets me to here … So it’s oscillating like it did before…. Something bad is happening … Each time I oscillate, I catch one of those, those arrows that’s steep enough to send me further and further away. And so this oscillates and goes away in its oscillations from the steady state. And so this diverges from the dynamical steady state in an oscillatory way, and so we’d say that the numerical solution is unstable.

So note here, though, that the dynamics are stable. The dynamics of the population is stable. It’s the numerical solution that’s unstable. This is the two aspects I was talking about before, two aspects of stability that matter to us when we’re modelling, for instance, population growth.

Figure scripts: plot_logistic_small_pert.m

Now, stability is usually defined in terms of the small perturbation. So we give our ball a tiny knock and see if it rolls down, right? So let’s, let’s look at stability with respect to a small perturbation.

Here we’re doing H equals 4.5 steps. So, imagine that we’re coming along just fine here … so our Euler’s method, when it’s on that 8, will stay at that 8, because it’s always changing by 0.

Now we perturb it a little bit, and we’ll have an oscillation…. And with each step, our bounce gets higher and higher … And so this one’s still diverging as well.

Before, I showed you us approaching the steady state, but really, we define stability with respect to a small perturbation near the steady state. You can see that, again, yes, it’s unstable, as we thought before.

In your lecture notes, in your online lectures, there’s a slide about this, and it talks about a mapping, G, and if it has a fixed point, and the key quantity here is … if the absolute value of G-Z is less than 1, then Z is stable.

And so this is confusing, because we were talking about stability before, and we were looking for derivatve less than 0 and greater than 0, and now we’ve got an absolute value ..

What’s going on here? What is the meaning of what’s happening here?

I could leave you on a cliffhanger. I’ve got fair bit of content to get through. Do you guys want a 5-minute break, or do you want to push through? Short break. Short break, excellent idea.

(Break)

Alright, so where were we? So we’ve got this idea of stability of the numerical method. And we have an example of the Euler’s method being unstable with respect to a small perturbation. And so, in our online lectures, we were told that we’re to take some derivative, find its absolute value, see that it’s less than 1, and that means it’s stable.

And we’re like, okay, but why?

Figure scripts: plot_cobweb_stable.m

The second friend I’m going to introduce you to tonight is called the cobweb plot. This is another visual tool, a bit like the quiver plot I showed you before, and it’s used for understanding something called a linear map.

So, you’ve seen this kind of thing before, where you have some value at the next step, and it’s equal to some function of the value at the previous step. And here we’ve got some Y stars, and that happens to be the fixed point, so I might write that in there, actually … Fixed point. Which means that if we start at Y star, then Y… n plus 1 will equal Y, N will equal Y star. And this is our G that’s, defined in the online lectures.

So, how would we go about solving this kind of visually? What I’ve done here is I’ve plotted, the one-to-one line. And here I’ve got YN, our previous step, and YN plus 1, our next step. And this here is .. the function G, up the top there. This is our fixed point where the two lines meet.

And so, how would we do this mechanically? So we might start at some Y0 value. And then to get to Y1, we evaluate, G at Y0. And so, that corresponds … to this point here. And so visually, we might … just draw a line to indicate that, and that’s our Y1. So the next step in this process is that we take our Y1 value, and we substitute it into G again to get our Y2. And so, we need to find … set our YN equal to Y … Y1, we can actually kind of draw a line there, and you see where that touches the one-to-one point, is where our new Y1 is? We can do a step to our next Y2, so we’ve marked that here…. And then we’re going to substitute our Y2 into G to get our Y3 … Y2, you’re going to go up, and that gives us our Y3 ..

And so you can see that this, staircase thing that I’m drawing is basically keeping a track of our Y1, Y2, Y3, and so on, values, and … it staircases into this point.

We can do it from the other end, if we’ve started here. We would go … Well, the point of these is usually to stop thinking, so you go … Vert G … horizontal 1 … vert G … horizontal 1 … And so on. So it’s a visual representation of using this iterative map.

Are there any questions about what I’ve drawn there? Does that make sense? I’m not getting a yes or a no. Okay, so the reason that I’m showing you this … yes, okay, great, thank you. It sort of makes sense.

It seems a bit less useful than the quiver, yeah? That’s because I haven’t told you how it’s useful yet.

Alright, so the reason that it’s useful, why am I telling you about linear maps, is because it turns out that Euler’s method is also an iterated function. It’s the same kind of thing, check it out. You’ve got here … YN .. YN … YN plus 1. It’s the same as before, YN over here … YN plus 1. And so that means that we could actually be drawing Euler’s method using this same kind of technique, right?

In your online lectures, you’ve got the Euler’s method on a Logistic Equation. So I’ve expanded it out here, just for convenience. And the first step is to write it as GY, so we’re replacing all these YNs with Ys. This is our G. And then you’re told that you take the derivative of G with respect to Y, evaluated at the steady state.

So in your online lectures, the notation used is this … So, hang on, what even is this? It’s okay, it’s the slope of G, it’s the slope of the Euler method at Y star.

So, if we were really, really close to our steady state, and we did a small perturbation, then we could kind of approximate what our map looks like as a line instead of the curve, and assume that the slope stays the same, provided we make our perturbation small enough. And so that’s the principle of stability analysis, it’s always with respect to a small enough perturbation that our maths is easy. And then we can use the slope of Y star.

So, let’s try applying this thing, and see if we can connect it back to the meaning.

Figure scripts: plot_logistic_euler_red.m

This was our example before, where we had H equals 1, and it converged nicely and smoothly towards the steady state, the dynamical steady state. And so, if we …

Figure scripts: plot_cobweb_stable.m

… take that, DGDY that we calculated before, and we substitute in H equals 0.5 … so we put an 0.5 in here … then we end up with 0.5 as our slope. And in fact that is giving us the same line as before that I did the cobweb plot on. I cheated, it’s the same example.

In this case, we know our Y star, it’s actually … equal to 8. And so what we do is we imagine ourselves perturbing our Euler’s method around this Y star just a little bit. So we start our perturbation here … And then we do … Just what we did before … visually.

And you see that even if we approach from above or below, our Euler’s method values get closer and closer to our Y star, until they’re kind of stuck there. And so this is our Euler’s method converging towards that dynamical steady state.

Figure scripts: plot_logistic_euler_red.m

Let’s take a look at the next example we had. This was when H equals 3.5, and it did converge, but it converged in this oscillatory way.

Figure scripts: plot_cobweb_osc_stable.m

So let’s use the derivative of G that we calculated before. We’re going to sub in here, this time, H equals 3.5 … so we put an 3.5 in here … and we get negative 0.75. So here’s our cobweb plot that we’re about to plot with the G slope at negative 0.75.

And so, if we do our iterations on this … so this here is, as before, Y star… Actually, I want to make that a little bit further down so that I’ll have space … And it’s the same on this side. So let’s say we start with our perturbation here at Y0, So we go … Up to here, this is our first Euler step, Y1. We’ll draw it on both axes. This is our next one, Y2 … Drew it on the other axis as well. That’s our Y3 … on axis as well. There’s our Y4 … Y5 … Y5 .. And so on.

Check it out. Looks like … Y0 was here… … Then for two, we jump to the other side. For three, we jump to the … of 1, I should say. For two, we jump to the other side, but a little bit closer. … 3, we jump to the other side, but a little bit closer …

It’s oscillating towards the steady-state. Which is exactly what we did when we looked at the quiver plots, right? It’s captured that dynamic for us.

Figure scripts: plot_logistic_euler_red.m

Let’s do one more example. So this was the one with H equals 4.5, and this one was unstable. It was oscillatory, and it diverged.

You think the cobweb plot looks cool? Yeah, same.

Figure scripts: plot_cobweb_unstable.m

So again, it’s the same thing. So we get … Our H equals 4.5, and we put it into our derivative here, and we’ve got negative 1.25, and so we’re drawing that line with a slope of negative 1.25.

This is our … Y star equals 8. Same thing here. This time, I’m going to start close. Because if I do the same process before … Horizontal 1, vertical blue, horizontal 1, Vertical G, horizontal 1, vertical G. You can see … there’s this same oscillatory thing happening, but the oscillations are getting bigger and bigger … And then it shoots off.

And so this cobweb plot and the pictures we’re drawing, is capturing what was happening in the Euler, in the numerical solutions dynamics.

At this point, are there any questions about what I’m doing there?

(A bit of back and forth with students)

… You all understand it really well. That’s good, because now you’re going to do your own.

Figure scripts: plot_cobweb_unstable.m, plot_cobweb_neg1.m, plot_cobweb_osc_stable.m, plot_cobweb_stable.m, plot_cobweb_pos1.m, plot_cobweb_gt1.m

Okay, I’m going to send you to a pair-and-share. I’m going to send you guys to a breakout room.

I have already done … This one … and this one … and this one. I want you guys to do this one…. This one … And this one. This one’s the important one.

While you’re in the breakout room. Think about what the cobweb plot would look like, and what that means for the dynamics of the numerical solution near whatever steady state this is representing. And while you’re there, I’ll draw my own back in there as well, so that you’ll have something to look at how to do it. I’m gonna send you all away.

(Pair and share in class, breakout rooms online)

Okay, cool. Alright, so let’s go through them one by one. So what happens in this one here? If I … start off here, what did you guys notice about the … the cobweb plot that you end up with for this one. Comes back to where it started. Did you guys in chat find the same thing?

Okay, so we had a question about what happens in the cobweb plot with this one, and someone in the room said that it comes back to itself, and so that is indeed the case, that we end up going round. And, I have to make sure my lines are straight, and then we’re just going around in a circle, like this.

Alright, what about this one here, where G … the derivative of G equals 1? What happens with the dynamics in this one? … Yeah, like, not a lot, hey. So if you start here, there’s a line underneath… Are you just kind of stuck there? But they have the same intuition. Would it be a series of boxes inside each other for each initial value? Yeah, it’d just be a point, because it’s just stuck there for each initial value. This is like a weird edge case on the one. We’re going to return to this point of it being the one.

How about this one? The final one.

The top center graph? Oh, I’m sorry. Oh, yes, yes, you were right. Exactly true, that you would … if you started here, you would have another little limit cycle … going around like this. All the way around. Yeah, sorry, I thought you meant the one that I was talking about, the bottom center. That’s exactly right. Thanks.

And how about the final one? What does the dynamics look like for this one? Maybe if we start from here, what did you guys find? … Chat, you can beat them if you’re quick. … We figured it would go across to the right, then up, and repeat. Across to the right. No, see, yeah, so this is the only trick to the cobweb plot, is that you’ve got to remember that if you’re starting at the 1 to 1 line, then you’ve got to go vertical first. So you’re actually gonna go down like this. Because I was drawing the others on the left-hand side, wasn’t I? I mean, I drew it on the right-hand side here, but you’d basically have to do that same pattern here. So instead, you’d be going vertical down, and then across to the left. And then vertical down. And across to the left. And so, in this case, your Euler solution, so it always starts from that diagonal bisector. … Yeah, yeah, so the reason is because, remember when I was talking about it before? I said that this is my Y0…. Y0 here … And this was my Y1. And so I represented that by the vertical line from the one to the … to the G…. Yep.

Alright, cool, so we’ve kind of looked at the space of all of the possible slopes of G, And … We can say that this one is unstable … Numerical solution, the Euler method is unstable. This one is stable … it oscillates inwards. This one is stable … It converges inwards smoothly. And this one here is unstable.

So the thing that’s separating them, turns out, it’s these very edge cases here, when the derivative of G With respect to Y is negative 1, when the derivative of G with respect to Y is 1.

And so now, you remember that your online lectures, there was this rule about the G Z … Less … absolute value … less than 1. And now you know where that 1 is coming from! That’s why 1 separates them out. That’s the meaning of the stability of the fixed point and the Euler solution.

There’s a Menti quiz on the screen right now, and I’d be really grateful if you could just scan it into your phones or something and take the quiz. The reason is that this course is under development, and I get some input into it. And so basically, it’s just asking you, have you seen this stuff before? Yes or no, and was it useful to you anyway, or if it was new to you, was it useful to you in general?

While we’re doing that, I’ll just talk about where we’ve been. We looked at the two ways that stability is relevant to population modelling.

The first way is the stability of the dynamics of the model itself. So, is a population at a steady state? Is that steady state for the population stable?

But then there’s also another layer that we put on top of it, which is our numerical method. We’re looking at Euler’s method only so far, but you will be looking at other methods in later online lectures. And all methods, eventually, are variations on Euler method, they build on this same principle, that you’re taking the derivative, you’re calculating the derivative and point, and you’re making some kind of jump.

You might be clever about it. You might take the average of derivatives over a space, or you might, go, oh, this derivative is too high, I’m going to take a smaller step at this point. But it’s all Euler methods at the bottom, all the way down.

And so we need to know about the stability of that numerical solution when it’s near the steady state, because, for instance, we might be interested in the step size. But then also later in the lectures, we leave this kind of iterative map to some really cool dynamics, like chaotic dynamics, period doubling chaos, which you’ll get a chance to look at in your practical.

That’s the end of that part, and now it’s time for activities…

In this post, I’ll show how the stationary distribution of actions taken during a repeated interaction can be found analytically and solved algorithmically using SymPy. The typical approach requires choosing a specific value for \(\varepsilon\), which is the probability that players make implementation errors. However, this choice is somewhat arbitrary if \(\varepsilon\) is introduced purely as a mathematical device to make the model tractable. My method avoids this arbitrariness by finding the limiting stationary distribution as \(\varepsilon \rightarrow 0\).

Kleshnina et al.’s paper concerns pairwise interactions that repeat over a number of rounds. The action that each player takes in each round is governed by their strategy, and it is a function of the actions in the previous round and the environmental state. If we assume that the probability \(\delta\) that the game continues for another round is high, then the payoff each strategy receives from interacting with each other strategy can be approximated. The approximation is made based on the stationary distribution of environment+action states when those two strategies interact.

To find the stationary distribution, Kleshnina et al. (2023) used a standard procedure, which is an approximate method. The Markov chain describing the sequence of environment+action states is not necessarily irreducible (e.g., Fig. 1). This means there are some states \(i\) that cannot reach another state \(j\) no matter how many rounds are played. Therefore, to find the stationary distribution, they assumed that in each round each player will make a mistake with probability \(\varepsilon\), playing cooperate instead of defect or vice versa. They set \(\varepsilon\) to a small fixed value, in their case \(\varepsilon = 0.01\), and modified the transition matrix accordingly. Then they found the left-eigenvector of the transition matrix numerically, which gives the stationary distribution.

Once all the stationary distributions between all pairs of strategies are found, the evolutionary dynamics can be solved. Each stationary distribution determines the payoff that both strategies receive when interacting with each other. These payoffs are then input to the evolutionary model, which describes how the population moves from fixation of one strategy to another over time. It is also a Markov chain model, and its stationary distribution gives the evolutionary steady state.

Fig. 2 below reproduces Fig. 3a from their paper, which shows the proportion of time selected strategies are at fixation at the evolutionary steady state. Some nodes in the figure are labelled with a binary string, which is a code that defines that strategy, while WSLS refers to the “win-stay lose-shift” strategy, and ALLD refers to “always defect”.

The strategy proportions in Fig. 2 were calculated based on \(\varepsilon = 0.01\), and those proportions will change when \(\varepsilon\) changes (Fig. 3). In particular, as \(\varepsilon\) approaches zero, the proportion of time the population that pursues the most frequent strategy almost halves, and the relative ordering of the time proportions changes as well.

Setting \(\varepsilon\) to some specific value may be valid depending on the question being asked. Nonetheless, in situations where \(\varepsilon\) is simply intended to represent “some small chance” of a mistake, then an intuitively attractive choice would be to find the solution as \(\varepsilon\) approaches zero. But that’s not something that’s easy to solve using numerical methods. It’s not obvious how close to \(\varepsilon = 0\) is “close enough”, and exploring the effects of different parameter values on the model is already computationally expensive. Furthermore, the smaller the value chosen for \(\varepsilon\) is, the more likely we are to run into numerical issues.

Instead, in the sections below, I detail how the stationary distribution as \(\varepsilon \rightarrow 0\) can be found analytically. In general, when the stationary distributions are found analytically, the evolutionary component of the model can predict quite different strategy proportions (Fig. 4). This also means that any conclusions we reach about which strategies are favoured by natural selection can depend on the method used.

The underlying principle to the analytic solution is illustrated in Example 1 below. Example 1 describes a somewhat different Markov chain scenario from the type they modelled, which I chose for its clarity. The section below works through a real example from their model, both by hand and in Python using SymPy.

Worked example

Consider a game played in the timeout environment

between two players, an All-Defect strategist

and a peculiar, mostly-defecting strategy who only cooperates when the previous action was DD

Worked example by hand

Index the states: (1) gCC, (2) gCD, (3) gDC, (4) gDD, (5) bCC, (6) bCD, (7) bDC, (8) bDD.

In a deterministic game played without any errors, the transition matrix is

where rows are predecessors, columns are successors, and the state vector is multiplied on left.

The dynamics has two attractors — \(\{ \text{gDD}, \text{bDC} \}\) and \(\{ \text{bDD}, \text{gDC} \}\) — and the Markov chain is not irreducible (Fig. 5a).

If players can make errors, then the Markov chain becomes irreducible (Fig. 5b). The transition matrix with the errors included is

For example, the \((1 - \varepsilon)^2\) in row \(i = 1\) (gCC) and column \(j = 4\) (gDD) means that the game will transition from gCC to gDD in the event that neither player makes an error, which occurs with probability \((1 - \varepsilon)^2\).

We can write the stationary distribution as a vector of polynomial functions of \(\varepsilon\)

where \(k_{i,j}\) is the coefficient of the \(j\)-th power of \(\varepsilon\) in the polynomial describing the stationary distribution of state \(i\). As \(\varepsilon \rightarrow 0\), \(\boldsymbol{v} \rightarrow \boldsymbol{v}_{\varepsilon \rightarrow 0} = (k_{1,0}, k_{2,0}, \ldots, k_{8,0})\), so we are interested in finding the \(k_{i,0}\) coefficients.

The normalisation for the stationary distribution gives our first equation

From Eq. \ref{Eq:stationary_distn_defn_v2}, we obtain 8 more equations

Grouping \(\varepsilon^0\) coefficients, we obtain 8 equations:

which, combined with the normalisation constraint (Eq.~\ref{Eq:normalised_k_0_to_7_v2}), can be reduced to the partial solution

An unknown in \(\boldsymbol{v}_{\varepsilon \rightarrow 0}\) remains, so we consider the coefficients of the next power of \(\varepsilon\), which is \(\varepsilon^1\).

Grouping \(\varepsilon^1\) coefficients, we obtain 8 more equations

Substituting Eqs. \ref{Eq:eps0_partial} into Eqs. \ref{Eq:eps1}, we obtain the remaining coefficients

Therefore, as \(\varepsilon \rightarrow 0\), the stationary distribution approaches

Worked example by code

Begin by defining the problem:

# A simplified script that calculates the solution for the worked example. 
#
# The example has:
#   - q = (1, 0, 0; 1, 1, 1)
#   - p0 = (0, 0, 0, 0; 0, 0, 0, 0), ID = 0
#   - p1 = (0, 0, 0, 1; 0, 0, 0, 1), ID = 17

import sympy as sp
import numpy as np


# parameters
# ---

# epsilon is the action-error probability defined as a symbolic variable
eps = sp.symbols("eps")

# we will try to solve by matching coefficients of epsilon powers up to eps^2
max_pwr = 2

# the 8 x 8 transition matrix between states including errors
# (normally generated by other code, but hardcoded here for clarity)
P = np.array(
    [
        [eps**2, eps*(1 - eps), eps*(1 - eps), (1 - eps)**2, 0, 0, 0, 0],
        [0, 0, 0, 0, eps**2, eps*(1 - eps), eps*(1 - eps), (1 - eps)**2],
        [0, 0, 0, 0, eps**2, eps*(1 - eps), eps*(1 - eps), (1 - eps)**2],
        [0, 0, 0, 0, eps*(1 - eps), eps**2, (1 - eps)**2, eps*(1 - eps)],
        [eps**2, eps*(1 - eps), eps*(1 - eps), (1 - eps)**2, 0, 0, 0, 0],
        [eps**2, eps*(1 - eps), eps*(1 - eps), (1 - eps)**2, 0, 0, 0, 0],
        [eps**2, eps*(1 - eps), eps*(1 - eps), (1 - eps)**2, 0, 0, 0, 0],
        [eps*(1 - eps), eps**2, (1 - eps)**2, eps*(1 - eps), 0, 0, 0, 0]
    ],
    dtype=object
)

The first step to finding the stationary distribution is to define all our coefficients as symbolic variables

# find the stationary distribution 
# ---

nbr_states = P.shape[0]

# matrix of epsilon coefficients, k_ij
#   - rows i correspond to the state
#   - columns j correspond to the power of epsilon
coeffs = [
    [sp.symbols(f"k{state_idx}{pwr}") for pwr in range(max_pwr + 1)]
    for state_idx in range(nbr_states)
]

This produces coeffs for \(\varepsilon\) up to the second power:

[[k00, k01, k02], [k10, k11, k12], [k20, k21, k22], [k30, k31, k32], 
 [k40, k41, k42], [k50, k51, k52], [k60, k61, k62], [k70, k71, k72]]

Define the stationary distribution as a polynomial in epsilon up to max_pwr

# the stationary distribution expressed as a polynomial in epsilon
# v_i = k_i0 eps^0 + k_i1 eps^1 + ...
v = np.array(
    [
        sum(coeffs[state_idx][pwr] * eps**pwr for pwr in range(max_pwr + 1))
        for state_idx in range(nbr_states)
    ]
)

This produces v as a polynomial up to the second power:

array([eps**2*k02 + eps*k01 + k00, eps**2*k12 + eps*k11 + k10,
       eps**2*k22 + eps*k21 + k20, eps**2*k32 + eps*k31 + k30,
       eps**2*k42 + eps*k41 + k40, eps**2*k52 + eps*k51 + k50,
       eps**2*k62 + eps*k61 + k60, eps**2*k72 + eps*k71 + k70],
      dtype=object)

Define the right-hand side of the stationary distribution equation

# at the stationary distribution, v = vP
rhsV = list(v @ P)

This produces rhsV:

[eps**2*(eps**2*k02 + eps*k01 + k00) + eps**2*(eps**2*k42 + eps*k41 + k40) + eps**2*(eps**2*k52 + eps*k51 + k50) + eps**2*(eps**2*k62 + eps*k61 + k60) + eps*(1 - eps)*(eps**2*k72 + eps*k71 + k70),
 eps**2*(eps**2*k72 + eps*k71 + k70) + eps*(1 - eps)*(eps**2*k02 + eps*k01 + k00) + eps*(1 - eps)*(eps**2*k42 + eps*k41 + k40) + eps*(1 - eps)*(eps**2*k52 + eps*k51 + k50) + eps*(1 - eps)*(eps**2*k62 + eps*k61 + k60),
 eps*(1 - eps)*(eps**2*k02 + eps*k01 + k00) + eps*(1 - eps)*(eps**2*k42 + eps*k41 + k40) + eps*(1 - eps)*(eps**2*k52 + eps*k51 + k50) + eps*(1 - eps)*(eps**2*k62 + eps*k61 + k60) + (1 - eps)**2*(eps**2*k72 + eps*k71 + k70),
 eps*(1 - eps)*(eps**2*k72 + eps*k71 + k70) + (1 - eps)**2*(eps**2*k02 + eps*k01 + k00) + (1 - eps)**2*(eps**2*k42 + eps*k41 + k40) + (1 - eps)**2*(eps**2*k52 + eps*k51 + k50) + (1 - eps)**2*(eps**2*k62 + eps*k61 + k60),
 eps**2*(eps**2*k12 + eps*k11 + k10) + eps**2*(eps**2*k22 + eps*k21 + k20) + eps*(1 - eps)*(eps**2*k32 + eps*k31 + k30),
 eps**2*(eps**2*k32 + eps*k31 + k30) + eps*(1 - eps)*(eps**2*k12 + eps*k11 + k10) + eps*(1 - eps)*(eps**2*k22 + eps*k21 + k20),
 eps*(1 - eps)*(eps**2*k12 + eps*k11 + k10) + eps*(1 - eps)*(eps**2*k22 + eps*k21 + k20) + (1 - eps)**2*(eps**2*k32 + eps*k31 + k30),
 eps*(1 - eps)*(eps**2*k32 + eps*k31 + k30) + (1 - eps)**2*(eps**2*k12 + eps*k11 + k10) + (1 - eps)**2*(eps**2*k22 + eps*k21 + k20)]

Now we find equations that we can use to solve for the stationary distribution. The first equation is the normalisation equation

# At the stationary distribution, v = rhsV.
# As the error eps -> 0, the stationary distribution approaches
# the epsilon-order 0 coefficients, i.e.,
#   v -> (k_10, k_20, k_30, ...)

# solve by matching epsilon-power terms

# first, from normalisation of the stationary distribution,
# we always have: 1 = k_10 + k_20 + k_30 + ...
pwr_2_eq0s = {
    0: [1 - sum(coeffs[state_idx][0] for state_idx in range(nbr_states))]
}

So far, we have pwr_2_eq0s:

{0: [-k00 - k10 - k20 - k30 - k40 - k50 - k60 - k70 + 1]}

The other equations are obtained from \(\boldsymbol{v} = \boldsymbol{v}P\).

# then, from v = vP, each state has an equation involving various
# epsilon-order terms:
#   k_i0 + k_i1 eps + ... = [term]_i0 + [term]_i1 eps + ...
for state_idx, rhs in enumerate(rhsV):
    pwrs_terms = rhs.as_poly(eps).all_terms()
    for pwr_tuple, term in pwrs_terms:
        pwr = pwr_tuple[0]
        if pwr <= max_pwr:
            eq0 = term - coeffs[state_idx][pwr]
            if eq0 != 0:  # exclude not-useful 0 = 0 equations
                pwr_2_eq0s.setdefault(pwr, []).append(eq0)

Now, pwr_2_eq0s:

{0: [-k00 - k10 - k20 - k30 - k40 - k50 - k60 - k70 + 1,
  -k00,
  -k10,
  -k20 + k70,
  k00 - k30 + k40 + k50 + k60,
  -k40,
  -k50,
  k30 - k60,
  k10 + k20 - k70],
 1: [-k01 + k70,
  k00 - k11 + k40 + k50 + k60,
  k00 - k21 + k40 + k50 + k60 - 2*k70 + k71,
  -2*k00 + k01 - k31 - 2*k40 + k41 - 2*k50 + k51 - 2*k60 + k61 + k70,
  k30 - k41,
  k10 + k20 - k51,
  k10 + k20 - 2*k30 + k31 - k61,
  -2*k10 + k11 - 2*k20 + k21 + k30 - k71],
 2: [k00 - k02 + k40 + k50 + k60 - k70 + k71,
  -k00 + k01 - k12 - k40 + k41 - k50 + k51 - k60 + k61 + k70,
  -k00 + k01 - k22 - k40 + k41 - k50 + k51 - k60 + k61 + k70 - 2*k71 + k72,
  k00 - 2*k01 + k02 - k32 + k40 - 2*k41 + k42 + k50 - 2*k51 + k52 + k60 - 2*k61 + k62 - k70 + k71,
  k10 + k20 - k30 + k31 - k42,
  -k10 + k11 - k20 + k21 + k30 - k52,
  -k10 + k11 - k20 + k21 + k30 - 2*k31 + k32 - k62,
  k10 - 2*k11 + k12 + k20 - 2*k21 + k22 - k30 + k31 - k72],
}

We write the list of coefficients we want to solve for

# we only want to solve the values of k_10, k_20, ...
wants = [coeffs[state_idx][0] for state_idx in range(nbr_states)]

This produces wants:

[k00, k10, k20, k30, k40, k50, k60, k70]

We incrementally increase the maximum epsilon power until we have an expression for each of the coefficients we want with no free symbols

# so we match epsilon terms, increasing the epsilon power
# incrementally, until we have taken into account enough rare
# sequences of errors that we can obtain the solutions we want
stationary_distn = list()
eq0s = list()
for pwr_level in range(max_pwr+1):
    
    # add to our system of equations 
    # coefficient-matching at current power level
    eq0s += pwr_2_eq0s[pwr_level]

    # solve system of equations for epsilon coefficients
    free_coeffs = set.union(*[eq0.free_symbols for eq0 in eq0s])
    soln = sp.solve(eq0s, free_coeffs) # returns [] if can't

    # check if solution has all the coefficients we want
    if all(want in soln for want in wants):
        # got an expression for each coeff we wanted
        stationary_distn_temp = [soln[want] for want in wants]
        if all([not propn.free_symbols for propn in stationary_distn_temp]):
            # each an expression we got had no unknown variables, so we're done!
            stationary_distn = stationary_distn_temp
            break

The loop above breaks at pwr_level = 1, giving soln:

{k00: 0, k01: 3/14, k10: 0, k11: 2/7, k20: 3/14, k21: k71 - 1/7, k30: 2/7, 
 k31: k61 + 5/14, k40: 0, k41: 2/7, k50: 0, k51: 3/14, k60: 2/7, k70: 3/14}

And so the stationary distribution as \(\varepsilon \rightarrow 0\) is stationary_distn:

[0, 0, 3/14, 2/7, 0, 0, 2/7, 3/14]

Future work

One thing I’m unclear about is how to determine the maximum power max_pwr that is needed to find the solution. My intuition tells me that the maximum power is probably the maximum number of errors needed to escape from one attractor to another, such that all attractors are eventually reachable. One could check only the states in each attractor for their shortest route to other basins. However, the shortest route of escape might pass through a transient state in the attractor’s own basin. Though even if that’s the case, it might not matter for much practical purposes; there’s no great harm in overestimating max_pwr, as I do in the example code above, it just means more computations.

I’m sure that someone has used this method before, but I haven’t been able to find it in the literature. I found a book Kato (1980), which has Chapter 2 dedicated to perturbation theory; however, the form of perturbation it considers is different from the one I use here. I also found Kandori et al. (1993), which has a very similar-looking polynomial; however, their method seems to require finding all possible structures they call “z-trees”, which is computationally expensive.

References

Kandori, M., Mailath, G. J. and Rob, R. (1993). Learning, mutation, and long run equilibria in games. Econometrica: Journal of the Econometric Society, 61(1):29-56.

Kato, T. (1980) Perturbation Theory for Linear Operators. Springer-Verlag, Berlin.

Kleshnina, M., Hilbe, C., Šimsa, Š., Chatterjee, K. and Nowak, M.A. (2023). The effect of environmental information on evolution of cooperation in stochastic games. Nature Communications, 14(1):4153.

I have taken an adjunct position there, in addition to my position at QUT, and I’m looking forward to regular visits to the lovely Nathan Campus, which is nestled in Toohey Forest.

In this blog post, first, I offer a proof of one of their propositions. Then I try thinking about their model a little differently to how they presented it, working through some small examples to try to get a visual intuition for what it means.

Signs of eigenvalues proof

Staab et al. (2022) model an \(n\)-player iterated public goods game with a continuation probability \(\delta\). Each round, individual \(i\) receives endowment \(e_i\) that they can either contribute to the public good or keep. Their strategy is deterministic and fixed for all rounds. If individual \(i\) contributes to the public good, their contribution is multiplied by their productivity \(r_i\). The return from the public good is shared among the members of the group according to a sharing rule \(\boldsymbol{f} = (f_1, \ldots, f_n)\), where \(f_i\) is the proportion of the jointly produced good that individual \(i\) receives.

The optimal sharing rule and minimum continuation probability pair \((\boldsymbol{f}^*, \delta_{\text{min}})\) solves an eigenvalue problem

where the matrix \(\Phi\) has elements

In Proposition 4, they state:

“the optimal sharing rule [\(f^*\)] is the eigenvector that corresponds to the largest eigenvalue of the matrix \(\Phi\)”

and

“the largest eigenvalue is the minimal continuation probability (\(\delta_{\text{min}})\) for this sharing rule to be feasible”

Below, I offer a proof that \(\delta_{\text{min}}\) is indeed the largest eigenvalue — the only eigenvalue that has the potential to be positive — and that it is positive only when their Assumption 1 is satisfied (non-triviality of cooperation):

The theorem can be proved by analysing the characteristic polynomial of \(\Phi\) using a similar approach to Meyer (2000, Ex. 7.1.22).

Proof. Matrix \(\Phi\) can be rewritten as a rank-one update of a diagonal matrix (e.g., Meyer, 2000, Sect. 6.2)

where \(D\) is a diagonal matrix with elements

and \(\boldsymbol{b}\) is a column vector with elements

Consider the corresponding eigenvalue problem

where \(\boldsymbol{1}^T \boldsymbol{v} = c\) is a constant. Rearrange to obtain \(1 = \boldsymbol{1}^T (\lambda I - D)^{-1} \boldsymbol{b}\). Since \(\lambda I - D\) is a diagonal matrix, \((\lambda I - D)^{-1}\) is also a diagonal matrix but with reciprocal elements to the original. Therefore, the eigenvalues solve \(1 = \sum_{i=1}^n \frac{b_i}{\lambda - d_i}\), which can be rearranged to obtain the characteristic polynomial of \(\Phi\):

To partition the repeated and unique eigenvalues, we factorise the characteristic polynomial \(f(\lambda)\). First, we index the unique diagonal elements of \(D\) in descending order \(d_{(1)} > d_{(2)} > ... > d_{(m)}\), where \(m \leq n\), and define the corresponding index sets:

Second, we define the sum of \(b_j\) elements in the same index set:

Then we can factorise the characterisic polynomial as \(f(\lambda) = g(\lambda) h(\lambda)\), where

and

The roots of \(g(\lambda)\) correspond to the repeated diagonal elements of \(D\), which are all negative. Specifically, for each unique diagonal element \(d_{(\ell)}\) with multiplicity \(|I_{(\ell)}| > 1\), \(g(\lambda)\) contributes \(|I_{(\ell)}| - 1\) roots to the characteristic polynomial \(f(\lambda)\), and these roots are equal to \(d_{(\ell)}\). The roots of \(g(\lambda)\) correspond to the eigenvalues of \(\Phi\) that are unchanged by the rank-one update. Since \(d_{(\ell)} < 0\) for all \(\ell\) (due to the definition of \(D\)), the roots of \(g(\lambda)\) correspond to negative eigenvalues of \(\Phi\). The total number of such eigenvalues is \(\sum_{\ell=1}^m (|I_{(\ell)}| - 1) = n - m\). Therefore, \(g(\lambda)\) accounts for \(n - m\) negative eigenvalues of \(\Phi\).

The remaining \(m\) eigenvalues are determined by the roots of \(h(\lambda)\). To characterise them, we will show that:

1. \(h(d_{(\ell)})\) alternates in sign with \(\ell\) according to: \(\text{sign}(h(d_{(\ell)})) = (-1)^\ell\) for \(\ell = 1, \ldots, m\).
2. \(h(L) > 0\) for sufficiently large \(L\).
3. \(h(0) < 0\) if and only if \(\sum_{i=1}^n \frac{1}{r_i} > 1\) (the reciprocal productivity condition).

To show Point 1, we analyse the signs of the terms in Eq. \ref{h(lambda)}. First, we can simplify \(h(d_{(\ell)})\)

From the ordering \(d_{(1)} > d_{(2)} > ... > d_{(m)}\), the signs of the terms in the product are known:

Therefore, \(h(d_{(\ell)})\) is the product of: the negative term \(-B_{(\ell)}\), \(\ell-1\) negative terms, and \(m - \ell\) positive terms. Consequently, \(\text{sign}(h(d_{(\ell)})) = (-1)^{\ell}\).

To show Point 2, we show that there exists some large-enough \(L\) such that \(h(L) > 0\). Rearranging Eq. \ref{h(lambda)}:

If \(L > d_{(1)}\), then the left-hand term \(\text{LHT} > 0\). If \(\sum_{i=1}^m \frac{B_{(i)}}{L - d_{(i)}} < 1\), then the right-hand term \(\text{RHT} > 0\). We observe:

Therefore, if \(L > m \cdot \text{max}(\{B_{(i)}\}) + d_{(1)}\), then \(h(L) > 0\).

To show Point 3, we substitute \(\lambda = 0\) into Eq. \ref{h(lambda)}

The left-hand term is positive. Therefore, \(h(0) < 0\) if and only if \(\sum_{i=1}^n \frac{1}{r_i} > 1\).

Using Points 1, 2, and 3 to analyse the sign of \(h(\lambda)\), we can locate the roots and identify the signs of the eigenvalues of \(\Phi\).

From Point 1, we know that \(h(\lambda)\) has \(m\) roots strictly interlacing the \(d_{(\ell)}\) values. The \(d_{(\ell)}\) values are negative. Therefore, \(m-1\) roots satisfy \(d_{(\ell + 1)} < \lambda < d_{(\ell)}\) and are negative.

The \(m-1\) negative roots of \(h(\lambda)\) combine with the \(n-m\) negative roots of \(g(\lambda)\) to account for \(n-1\) eigenvalues of \(\Phi\). Therefore, we can conclude that at least \(n-1\) eigenvalues of \(\Phi\) are negative.

The remaining root of \(h(\lambda)\) might satisfy either \(\lambda < d_{(m)}\) or \(\lambda > d_{(1)}\). From Point 2, since \(h(d_{(1)}) < 0\) and \(h(L) > 0\) for some large \(L\), then the remaining root must be the largest root of \(\Phi\) and satisfy \(d_{(1)} < \lambda_1 < L\). Therefore, in summary so far, we have

The sign of \(\lambda_1\) is determined by the sign of \(h(0)\). In particular, \(\lambda_1 > 0\) if and only if \(h(0) < 0\). From Point 3, \(h(0) < 0\) if and only if \(\sum_{i=1}^n 1/r_i > 1\), where the latter is the reciprocal productivity condition from Assumption 1 (Eq. \ref{reciprocal_productivity_condition}). Therefore, we conclude that \(\lambda_1 > 0\) if and only if Assumption 1 is satisfied.

Try to get a visual intuition

The folk theorem tells us that, if players in an iterated game are sufficiently patient (i.e., the discount factor \(\delta \rightarrow 1\)), then any feasible and individually rational average payoff can be sustained in a subgame-perfect equilibrium via a generalised Grim-trigger strategy. In particular, taking into account that the Nash equilibrium of the stage game NE is a subgame-perfect equilibrium, then a player will be willing to stick to any alternative strategy to NE, call it ALT, so long as the payoff from ALT is greater than or equal to the maximum payoff they could obtain from a one-shot deviation (MAX DEVN) plus reversion to NE for the remainder of the game

The following equation is given (between Eqs. 1 and 2 in Staab et al.) for the Grim strategy

We could generalise this a bit to obtain the space of feasible rational payoffs of all alternative strategies.

First, the frontier of the feasible set is defined by the payoffs from full cooperation with \(\sum_i f_i = 1\). Second, the maximum possible payoff that focal player \(k\) can obtain from a one-shot deviation occurs when: player \(k\)’s deviation is to defect instead of cooperate, and the deviation is timed to occur when all non-focal players choose cooperate. Therefore, the right-hand side of Eq. \ref{eq:staab_1.5} defines the bounds of the individually rational set. Therefore, the set of feasible and rational alternative-strategy payoffs are the values between the left- and right-hand sides of Eq. \ref{eq:staab_1.5}

When \(\delta = 1\), Eq. \ref{eq:my_staab_1.5} reduces to

where \(\boldsymbol{e}\) has the natural interpretation as the disagreement point.

As \(\delta\) increases, the space between the left- and right-hand sides Eq. \ref{eq:my_staab_1.5} contracts until we find the point where

It is finding this point that is the main focus of Staab et al.; in particular, finding the value of the pair \((\boldsymbol{f}^*, \delta^*)\).

A visual example

Consider a 2-player scenario where

At full cooperation, the maximum possible quantity of goods is produced

When those goods are efficiently shared, i.e., \(f_1 + f_2 = 1\), each player receives

This describes the function that defines the upper limit of the feasible set, i.e., the frontier, which is shown as a blue line in Fig. 1.

If the game is repeated forever, i.e., the continuation probability \(\delta = 1\), then the maximum deviation payoff players can receive is equal to the payoff from private investment

For each player \(k\), this is the minimum game payoff that a rational player should be willing to receive from the game, which are shown by red lines in Fig. 1.

Combining the upper limit defining the feasible set and the lower limits defining the minimum individually rational payoffs for all players defines the feasible and rational payoffs region (shaded red in Fig. 1). Any combination of strategies and sharing agreements (\(\boldsymbol{f}\)) that provide payoffs within this region can be sustained.

If the continuation probability \(\delta < 1\), then the maximum deviation payoff (normalised) includes the payoff from the deviation-round itself

Therefore, decreasing \(\delta\) shrinks the feasible rational region (e.g., when \(\delta = 0.5\), the region shrinks to the blue shaded region in Fig. 1), which reduces the number of strategies and sharing agreements that can be sustained.

Staab et al. are interested in finding the \(\delta_{\text{min}}\) for which the feasible-rational region shrinks to a single point. In Fig. 1, this point occurs when \(\delta = \delta_{\text{min}} = 0.13\), which corresponds to payoffs \((\pi_1^*, \pi_2^*) \approx (0.58, 1.02)\) on the frontier, with sharing agreement \((f_1^*, f_2^*) \approx (0.36, 0.64)\).

Some more examples

Productivities equal, vary outside options

Consider an example with equal productivities

where we vary the outside options (Fig. 2). The poorer player receives the smaller share, e.g., for the purple line, Player 1 is the poorer player.

We can predict the outcomes of higher and lower productivity levels — while keeping \(r_1 = r_2\) — by moving the frontier (blue line) up and down. When productivities are low, \(\delta_{\text{min}} \rightarrow 1\), and the shares reflect the outside option. But as productivity increases, \(\delta_{\text{min}}\) decreases, and the shares become more equal. The shares meet at equal shares, which occurs when \(r\) is high enough that it no longer presents a social dilemma. At this point, \(\delta_{\text{min}} = 0\), which makes this a one-shot game.

What does it mean that players demand an equal share in the one-shot game, regardless of their outside option? When \(\boldsymbol{r} = (2, 2)\), the payoffs they receive from the game are greater than their outside options. But recall that the fact a cooperative solution gives both players higher payoffs is not enough to guarantee it. From the eigenvalues proof, we need the leading eigenvalue \(\lambda_1 = 0\), which implies \(h(0) = 0\), which implies \(\sum_i 1/r_i = 1\). For equal \(r_i\), that implies \(r_i = 2\). The social dilemma condition is that the return on investment is less than one

and, when \(r_k = 2\), this condition is only satisfied by \(f_k = 0.5\).

Or to think about it another way, when \(r_i = 2\), the situation is on the cusp of transition from PD to mutualism. The payoff matrix is

where the calculation for the cooperative payoff is

and the deviations (off-diagonal elements of the payoff matrix) are

and

Productivities unequal

In this final subsection, I tried playing around with an example with unequal productivities, approaching it from different angles to see if it could help my intuition.

Consider an example with unequal productivities

and use Fig. 3 as our guide. I’m curious about the point where the disagreement-point trajectory hits the diagonal line, the special points marked with stars in Fig. example_3 and the grey line they align upon.

The dashed lines are equivalent to other full-cooperation payoffs when the \(r_i\) are increased but kept at the same ratio. For this example

From my eigenvalue equation, I know that \(\delta_{\text{min}} = 0\) when \(h(0) = 0\), which occurs when

This describes the dashed line where the star-points occur. Solving Eq. \ref{const_ratio} and Eq. \ref{lift_line} simultaneously, I obtain

I also know that, at the cusp of the transition from PD to mutualism, \(f_k \; r_k = 1\). Therefore,

I took the long route to get here. One can also get this equation by subbing \(\delta = 0\) into the \(f_k\) equation with any \(r\) values provided we use the same goods equation because we’re keeping the \(r\) ratios constant.

Anyway, in this example

For any given \(\boldsymbol{e}\), the equation for the maximum public good produced is

So I can find the star-points on the graph with

All star points land on a line that runs through the (0, 0) point and the special disagreement point. This line has slope \(f_2^{\star}/f_1^{\star}\) in share space, which is equal to its slope in payoff space \(\pi_2^{\star}(\boldsymbol{e})/\pi_1^{\star}(\boldsymbol{e})\) for all \(\boldsymbol{e}\).

When \(\delta = 1\), the line in payoff space will run through the disagreement point, which allows us to find the \(\boldsymbol{e}\) for which the shares do not vary with \(\boldsymbol{r}\) (keeping ratios constant) nor with \(\delta\)

This doesn’t help us find the \(f_i^*\) and \(\delta_{\text{min}}\); finding that intersection requires finding the equation for the dotted line. But it does explain when shares won’t change, and helps us have an intuition about where the shares are “heading towards” depending on \(\boldsymbol{e}\) relative to \(\boldsymbol{e}^{\star}\). For a given \(\boldsymbol{e}\), as \(\boldsymbol{r} \rightarrow \boldsymbol{r}^{\star}\), \(\boldsymbol{f} \rightarrow \boldsymbol{f}^*\).

Let’s now look at the special disagreement point from another angle. The trajectory of the disagreement point is defined by

The special points occur when \(\delta = 0\), when

which is then substituted into the payoff to get the special payoff points

Note, however, that \(f_k^{\bullet}\) is independent of the \(\boldsymbol{e}\) values. Therefore, provided the \(r\)-ratios are kept constant, all \(\boldsymbol{e}\) scenarios head towards the vector defined by by the \(f_k^{\bullet}\) values, i.e.,

When this is normalised, we obtain the special disagreement point, \(\boldsymbol{e}\), whose sharing rule is independent of the magnitude of the productivity vector, \(|\boldsymbol{r}|\). It is the endowment point for which the dotted-line trajectory is straight (coincides with grey line). The special endowment values are

Interpretation: as the magnitude of productivies increases, the solution heads towards the egalitarian solution to the special-endowment-value game with social indices in proportion to the players’ productivities (less productive players have a higher social index).

References

Meyer, C. D. (2000). Matrix analysis and applied linear algebra, Society for Industrial and Applied Mathematics, Philadelphia.

Staab, M., Kleshnina, M., Hübner, V., Hilbe, C. and Chatterjee, K. (2022). Optimal sharing in social dilemmas. URL: http://manuelstaab.com/research/optimal sharing soc dilemma.pdf

I extend my sincere thanks to the organisers – Alex McAvoy, Olivia Chu, and Daniel Cooney (bsky) – for their kind invitation and organising the workshop. The presentations in my session were all very interesting.

Maria Kleshnina's talk

Maria Kleshnina presented an overview of her recent work on iterated games. I’m particularly intrigued by her model where player behaviour receives feedback from the environment, which I’ve previously discussed on my blog here. She also discussed the concept of endowment distributions and sharing rules that are resilient to variation in the continuation probability. I’ve recently been studying the latter through her manuscript.

Anuraag Bukkuri's talk

Anuraag Bukkuri presented a model for cancer-cell dynamics using a stage-structured adaptive dynamic approach. While I’ve done a little work using the adaptive-dynamics framework, my focus has been on traditional eco-evolutionary applications. I had no idea that it could also be used to design more effective cancer treatments, which was a wonderful thing to learn.

Dini Wang's talk

Dini Wang (Github, manuscript presented) presented an exploration of evolutionary games on hypergraphs. While there’s extensive literature studying the evolution of cooperation on networks, hypergraphs have received comparatively less attention. A hypergraph extends the concept of a simple graph: rather than players being connected solely through pairwise edges, they form potentially overlapping groups. These group relationships can be represented by hyperedges, which are edges capable of connecting more than two nodes simultaneously.

The hypergraph structure influences both the payoffs players receive and the strategy-update process in evolutionary dynamics. For example, if you belong to two groups, you participate in two games, with your overall payoff being a combination from both games. Hypergraphs also allow for more possibilities in the strategy-updating process than a regular graph. For example, in the social-learning dynamics, when choosing which high-payoff individual to imitate, one might first select an outstanding group and then randomly select an individual from within this group.

Dini comprehensively explored different combinations of update rules made possible by the hypergraph structure, and she presented findings on which structures promoted cooperation and which updating rules were most effective (details in her manuscript). I was particularly struck by her discovery that, compared to simple graphs, the higher-order interactions facilitated by hypergraph structures are more conducive to cooperation. This was my first introduction to hypergraphs, and they appear to offer a more natural framework for describing human interactions than pairwise connections, so I’m excited to read her manuscript in more detail.

Saptarshi Pal's talk

Finally, Saptarshi Pal presented on different conceptualisations of resilience in subgame perfect Nash equilibria as they relate to symmetric 2-player, 2-strategy iterated games. His work focused on infinite iteration (continuation probability \(\delta = 1\)) and memory-1 strategies. All of these concepts are new territory for me, which means my interpretations of them below are likely wrong — please ask him for his manuscript to be sure.

The first concept was the resilient strategy, which strengthens the notion of a SPNE. When both players adopt such a strategy, at no point in the game does any player have an incentive to deviate. Or, to put it another way, the strategy is independent of the history that has occurred up to this point, and the condition being met is robust to variation in that history.

The second concept was the stably resilient strategy, which maintains its resilience even when the game’s payoffs are perturbed. This can be viewed as a strategy that remains a best response even when players face uncertainty about exact payoffs. Interestingly, it appears that virtually every resilient strategy is also stably resilient, and the set of stably resilient strategies consists of just four types: self-cooperators, self-defectors, and two forms of alternators.

The final concept was the most intriguing — the prediction-proof strategy — which is a strategy that remains resilient even against opponents who can anticipate the player’s next move. While “seeing the future” might seem far-fetched, Saptarshi provided the real-world example of tennis champion Andre Agassi, who gained an advantage over Boris Becker by noticing that Becker unconsciously signalled the direction of his serves with his tongue. It seems likely we broadcast many signals about our intentions, both consciously and unconsciously.

As a concrete example, consider the coordination game with payoffs \((R, S, T, P) = (1, 0, 0, 1)\), where everyone ideally wants to play CC or DD. Flipping a coin is a resilient strategy if one’s partner only looks at history. However, if they have a strategy that conditions on your future move, then their deviation payoff is higher (1 > 1/2), and so this SPNE is not a prediction-proof strategy. The concept of a prediction-proof strategy is also applicable to situations where the stage game is not simultaneous because the follower “predicts” what the leader has done by having already seen it.

Saptarshi showed that these strategy types form a nested hierarchy: stably resilient \(\subseteq\) prediction proof \(\subseteq\) resilient \(\subseteq\) SPNE. In addition, the stably resilient strategies (or one of them?) are socially optimal, having the maximum total payoffs of all memory-1 games. This clean result allows for a clear definition of the optimal strategy. Saptarshi plans to extend this work to scenarios where \(\delta < 1\).

My talk

I presented an overview of my recent work developing mathematical techniques for analysing the evolution of cooperation in group games with family members. My slides are available here.

Modellers using the Qualitative Modelling approach often model a species eradication as a press-perturbation. This is obviously wrong, but it’s convenient and has a certain intuitive appeal, and it’s not known how often it gives answers that are wrong enough to matter.

In this blog post, I provide a fast method to predict the effects of an eradication using the community matrix alone. A worked example is provided at the end. The key assumption is that the underlying species dynamics are Lotka-Volterra.

This blog post might provide a starting point for investigating how the predictions of modelling a press-perturbation differ from eradication-proper, and for determining when it matters.

Background

The Lotka-Volterra system

Consider an ecosystem with \(S\) species, and denote the population size of species \(i\) at time \(t\) by \(n_{t;i}\).

We assume the system can be approximated by Lotka-Volterra dynamics

where \(r_i\) is the intrinsic growth rate of species \(i\) and \(b_{i,j}\) is the interaction strength between species \(i\) and \(j\). If species \(j\) has a negative effect on species \(i\), then \(b_{i,j} < 0\), otherwise \(b_{i,j} > 0\), and \(b_{i,j} = 0\) indicates that there is no direct interaction between the species.

The coefficients can be written in vector and matrix form; \(r = (r_1, r_2, \ldots, r_S)\) and \(B_{i,j} = [b_{i,j}]\). Then the dynamics described by Eq. 1 has a single steady state \(n = (n_1, n_2, \ldots, n_S)\), which is solved by

The stability of the steady state is determined by investigating the eigenvalues of the Jacobian matrix

where \(N\) is the diagonal matrix formed of the vector of steady-state population sizes \(n\) and the partial derivates are evaluated at the steady state. If the maximum real part of the eigenvalues is negative, then the steady state is locally stable.

The scaled Lotka-Volterra system

The dynamical system (Eq. 1) can be scaled with respect to the steady state. Denote the scaled population sizes

Then the scaled system

with the new steady state \(x = (1, 1, \ldots, 1)\).

The new Jacobian matrix — also known as the ‘community matrix’ — is equal to the matrix of scaled interaction terms

Qualitative modelling typically starts with the community matrix \(A\), which represents the dynamics linearised around the steady state. In the case where the underlying dynamics are Lotka-Volterra, the relationship between the original dynamical system and the scaled system has some noteworthy properties:

(1). Each \(A\) corresponds to a family of Lotka-Volterra systems with different \(B\) and \(n\) satisfying Eq. 6. This matters if you are uncertain about the parameter values but want to make some probabilistic predictive statements about how the system is likely to behave. For example, if you want to say something “80% of the time, the predictions of the press-perturbation match the eradication predictions”, then you need to think very carefully about this point (see: Kristensen et al. 2019).

(2). If it is assumed that all species are present in the system at steady state, i.e., \(n_i > 0 \; \forall i\), then the signs of the elements of \(A\) correspond to the signs of the direct interactions between species.

(3). Substituting Eq. 3 into Eq. 6, we obtain

which is a similarity transform. Therefore, the eigenvalues of \(J\) are equal to the eigenvalues of \(A\).

(4). At the steady state

so the signs of the intrinsic growth rates can also be determined from \(A\). This might be useful for parameterising the system. For example, if there is a predator species being modelled that has no prey items outside the model, then its growth rate should be negative.

The effect of species eradication

Qualitative modelling often looks at the effects of a constant outflow (or inflow) of a species on the other species in the ecosystem. This is called a press perturbation, and modelling it involves investigating the signs of the elements of the inverse of \(A\) (Bender et al. 1984, Nakajima 1992). For example, Raymond et al. (2011) simulated the eradication of invasive species from Macquarie Island in this way.

However, a press perturbation of an invasive species is different from removing that species altogether. We have no reason to suppose the effect of removing a target species on other species will have the same signs, i.e., positive or negative effects on their population sizes, as removing a small (infinitesimally small!) number of the target species from the system at a constant rate.

Nonetheless, if we assume that the underlying dynamics of the system are Lotka-Volterra, there is another way we can know about the effects of an eradication using the community matrix \(A\) directly. In short, provided that no other species are sent extinct by the eradication, then we can predict both the proportional change in steady-state population sizes and the stability of the new steady state from the community matrix of the old system alone.

Proportional change in steady-state population sizes

Consider the eradication of species \(k\). Let us use subscript \(\ell \neq k\) to denote a vector or matrix modified by removing the \(k\)-th row or column as applicable. Let us denote the steady-state population sizes in the old system by \(n\) as before. Let us denote the post-eradication steady-state population sizes by \(p = (p_1, p_2, \ldots, p_{k-1}, p_{k+1}, p_S)\), which is a vector of length \(S-1\). We are interested in the proportional change in the population size of species \(i\) due to the removal of species \(k\), which is defined as

In the old-system, the steady-state population sizes of the species who are not eradicated, \(n_{i \neq k}\), is our baseline of comparison. Eq. 2 can be rewritten

and so

Note that to calculate \((B_{i \neq k, j \neq k})^{-1}\) in Eq. 10, the rows and columns are removed first before the inversion is performed, and the same applies to all other bracketed inversions below.

At the new steady-state post-eradication, the steady-state population sizes of the other species is solved by

Therefore, the change in the steady-state population sizes of the other species due to eradication of species \(k\) is

From Eq. 6, we have

The final step above is possible because \(N\) is a diagonal matrix, and so its inverse is also a diagonal matrix whose nonzero elements are reciprocal to the original, i.e., \(n_{i,i} \rightarrow 1/n_{i,i}\). Therefore, \((N^{-1})_{i \neq k, j \neq k} = (N_{i \neq k, j \neq k})^{-1}\). Let us denote the inverse submatrix of \(N\) by simply \(N_{i \neq k, j \neq k}^{-1}\) for brevity and to remind us of this fact.

Substituting Eq. 13 into Eq. 12 \(\begin{align} A_{i \neq k, j \neq k} \; N_{i \neq k, j \neq k}^{-1} \; (p - n_{i \neq k}) &= A_{i \neq k, k}, \\ p - n_{i \neq k} &= N_{i \neq k, j \neq k} \; (A_{i \neq k, j \neq k})^{-1} \; A_{i \neq k, k}. \tag{14} \end{align}\)

Substituting Eq. 14 into Eq. 8, we discover that the effect of eradication of species \(k\) on the steady-state population sizes of the other species can be determined from the old community matrix alone

In the situation where multiple species are eradicated at once, denote the set of eradicated-species’ indices \(K\), then the result can be generalised to

Stability of the new steady state

Eq. 15 tells us about how the new steady-state population sizes differ from the old ones, but we might also be interested in whether the new steady state is stable. For that, we need to investigate the Jacobians of the new system.

Let us denote the new Jacobian and new scaled community matrices by \(\hat{J}\) and \(\hat{A}\), respectively. Let us derive the new \(\hat{A}\), and let us also check \(\hat{A}\) has a similarity-transform relationship with \(\hat{J}\), like in Eq. 6.5, which will ensure that the eigenvalues of \(\hat{A}\) are equal to the eigenvalues of \(\hat{J}\).

The elements of the new post-eradication Jacobian are

and so the new Jacobian is related to the old Jacobian by

The elements of the new scaled Jacobian / community matrix are

and so the new community matrix is related to the old community matrix by

Can we use \(\hat{A}\) to calculate the eigenvalues of \(\hat{J}\)? We observe \(\begin{align} \hat{A} &= A_{i \neq k, j \neq k} \; \text{diag}(\delta + 1), \\ &= N^{-1}_{i \neq k, j \neq k} \; J_{i \neq k, j \neq k} \; N_{i \neq k, j \neq k} \; \text{diag}(\delta + 1), \\ &= N^{-1}_{i \neq k, j \neq k} \; \text{diag}(\delta + 1)^{-1} \; \hat{J} \; N_{i \neq k, j \neq k} \; \text{diag}(\delta + 1), \\ &= \underbrace{N^{-1}_{i \neq k, j \neq k} \; \text{diag}(\delta + 1)^{-1}}_{X^{-1}} \; \hat{J} \; \underbrace{\text{diag}(\delta + 1) \; N_{i \neq k, j \neq k}}_{X}, \tag{18} \end{align}\)

which is a similarity transform. Therefore, the eigenvalues of \(\hat{J}\) are equal to the eigenvalues of \(\hat{A}\). Furthermore, because we can determine the new community matrix \(\hat{A}\) from the old community matrix \(A\) alone (Eq. 17), then we can determine the stability of the new system from old community matrix alone.

Comments on the method

When a species eradication causes another species to go extinct

Eq. 15 gives the proportional change in the steady state, and if \(\delta_i < -1\), then species \(i\)’s new steady-state population size is negative. The real system cannot have species with negative population sizes — the least size is zero — and so Eq. 11 no longer applies.

What should we do in such a situation? The most rigorous way to determine the outcome would be to track the population dynamics. However, we might also expect that negative species are the species that went extinct, and so we could re-use maths above to study a system with those species removed. Whether or not this expectation is generally correct, however, is something we might want to check.

What happens when species go extinct in the press-perturbation analysis? In fact, the press-perturbation analysis overlooks this possibility entirely. The press-perturbation analysis does not simulate eradications (though it’s often used for that purpose), but instead simulates a continuous removal of an infinitesimally small number of the target species. When only an infinitesimally small number of individuals are removed (or added), then only infinitesimally small changes in the population sizes of other species result, and no species ever goes extinct.

Scaling

Qualitative modelling often involves Monte Carlo simulations, which means randomly sampling the magnitudes of the elements of \(A\) from some bounded range according to some distribution, e.g., a uniform distribution \(a_{i,j} \sim U(0, 1)\), and looking at the distribution of outcomes. Therefore, we might be concerned about whether or not limiting the magnitudes of \(A\) to some bounded range affects the outcomes we’re sampling.

Consider some scaling factor \(\alpha\) that has been applied to the true community matrix \(T\), i.e., \(A = \alpha \; T\), which was done in order to guarantee that \(|a_{i,j}| \in (0, 1)\) for all \(i\), \(j\). We know the signs of the eigenvalues will be preserved, \(\text{eig}(\alpha \; T) = \alpha \; \text{eig}(T)\), so the stability analysis will be preserved. Happily, we can also show the proportional change in steady-state population sizes due to eradications will also be preserved.

Specifically

so \(\delta_i\) is not affected by the scaling factor.

Worked example

The purpose of this example is to verify the maths above and provide a starting point for future analysis.

Let us consider the classic apex-predator + mesopredator + prey system, depicted in Figure 1. This system is particularly important to invasive-species eradication, e.g., cats + rats + native species, because conservation interventions to eradicate the apex-predator species (e.g., cats) can cause an increase in the mesopredator abundance (e.g., rats) and lead to worse outcomes for the prey (e.g., native species) than if nothing had been done.

Label the three species:

1. apex predator
2. mesopredator
3. prey

and let us assume the system obeys Lotka-Volterra dynamics with coefficience \(r\) and \(B\) defined below.

# Code is written in Python

import numpy as np
import matplotlib.pyplot as plt

# number of species
S = 3

# intrinsic growth rates
r = np.array([-0.09868652, -0.10491318,  1.24977311])

# Lotka-Volterra interaction terms
B = np.array(
    [
        [-8.28410720e-03,  2.81792972e-03,  1.11307405e-02],
        [-4.39125000e-05, -1.12271716e-03,  1.94991860e-02],
        [-6.15708830e-03, -5.27941320e-04, -2.51039475e-02]
    ]
)

At the steady state, the population sizes are:

n = np.linalg.inv(B) @ (-r)
print(n)

[100. 250.  20.]

The Jacobian evaluated at the steady state:

J = np.diag(n) @ B
print(J)

[[-0.82841072  0.28179297  1.11307405]
 [-0.01097812 -0.28067929  4.8747965 ]
 [-0.12314177 -0.01055883 -0.50207895]]

The eigenvalues of the Jacobian:

J_eigs = np.linalg.eigvals(J)
print(J_eigs)

[-0.99815469+0.j         -0.30650713+0.52456685j -0.30650713-0.52456685j]

The maximum real part of the eigenvalues is negative, so the steady state is stable.

Let’s check if the eigenvalues of \(A\) match \(J\).

The scaled community matrix \(A\):

A = B @ np.diag(n)
print(A)

[[-0.82841072  0.70448243  0.22261481]
 [-0.00439125 -0.28067929  0.38998372]
 [-0.61570883 -0.13198533 -0.50207895]]

\(A\)’s eigenvalues are

A_eigs = np.linalg.eigvals(A)
print(A_eigs)

[-0.99815469+0.j         -0.30650713+0.52456685j -0.30650713-0.52456685j]

So we have verified that \(A\) has the same eigenvalues as \(J\).

Check that scaling the dynamics works

Let us verify that the dynamics described by \(B\) and by \(A\) are the same.

We will start both systems with population sizes 1/10 of their value at steady state, and track how the population sizes change over time.

First, let’s do the original Lotka-Volterra system:

from scipy import integrate

# define the original dynamics
def dn_dt(n_t, t=0):
    return n_t * (r + B @ n_t)

# time range to plot the dynamics over
t = np.linspace(0, 20, 100)

# initial values for the population sizes
n_t_0 = 0.1 * n

# integrate numerically
n_t, infodict = integrate.odeint(dn_dt, n_t_0, t, full_output=True)
print(infodict["message"])

# plot
plt.plot(t, n_t, label=["apex", "meso", "prey"])
plt.title('Using B')
plt.xlabel('Time')
plt.ylabel('Unscaled population sizes')
plt.legend(loc="best")
plt.show()

Integration successful.

We want to compare to scaled results, so let’s scale the plot by dividing through by the steady-state population sizes:

plt.plot(t, n_t/n, label=["apex", "meso", "prey"])
plt.title('Using B')
plt.xlabel('Time')
plt.ylabel('Scaled population sizes')
plt.legend(loc="best")
plt.show()

Now let’s do the dynamics of the scaled Lotka-Volterra system using the community matrix \(A\):

# define the scaled dynamics
def dx_dt(x_t, t=0):
    return x_t * (r + A @ x_t)

# initial values for the population sizes
x_t_0 = 0.1 * np.ones(3)

# integrate numerically
x_t, infodict = integrate.odeint(dx_dt, x_t_0, t, full_output=True)
print(infodict["message"])

# plot
plt.plot(t, x_t, label=["apex", "meso", "prey"])
plt.title('Using A')
plt.xlabel('Time')
plt.ylabel('Scaled population sizes')
plt.legend(loc="best")
plt.show()

Integration successful.

Figs. 2 and 3 are the same, which verifies that the scaling preserves the dynamics.

Check method for species eradication works

Let’s now check that our equation for \(\delta_i\) (Eq. 15) is correct. First, let’s remove a species in the original system and see how it changes the population steady states. Then, let’s see if we can obtain the same proportional changes from the scaled community matrix alone. Let us remove the apex predator, species 1.

Our old interaction matrix and intrinsic growth rates were:

print("B = ")
print(B)
print("\nr = ")
print(r)

B = 
[[-8.28410720e-03  2.81792972e-03  1.11307405e-02]
 [-4.39125000e-05 -1.12271716e-03  1.94991860e-02]
 [-6.15708830e-03 -5.27941320e-04 -2.51039475e-02]]

r = 
[-0.09868652 -0.10491318  1.24977311]

When we remove the apex predator, our \(B_{i \neq 1, j \neq 1}\) and \(r_{i \neq 1}\) will be:

B_rem = B[1:S, 1:S] 
print("new B = ")
print(B_rem)

# Note: Python indexes elements from 0, while Matlab indexes from 1.
# If you were to do this in Matlab, you'd do something like
#   B_rem = B(2:S, 2:S)

r_rem = r[1:S]
print("\nnew r = ")
print(r_rem)

new B = 
[[-0.00112272  0.01949919]
 [-0.00052794 -0.02510395]]

new r = 
[-0.10491318  1.24977311]

Therefore, the new population steady state is:

p = np.linalg.inv(B_rem) @ (-r_rem)
print(p)

[564.8740935   37.90450627]

And the proportional changes in the other species steady-state population sizes is:

delta = (p - n[1:S]) / n[1:S]
print("Proportional change from original Lotka Volterra equations:")
print(delta)

Proportional change from original Lotka Volterra equations:
[1.25949637 0.89522531]

We find that, when the apex predator is eradicated, both the meso-predator’s and prey’s population size increases.

Can we get the same \(\delta\) using Eq. 15 above? Let’s try.

Recall Eq. 15 says: \(\delta = (A_{i \neq k, j \neq k})^{-1} \; A_{i \neq k, k}.\)

Recall our \(A\) was:

print(A)

[[-0.82841072  0.70448243  0.22261481]
 [-0.00439125 -0.28067929  0.38998372]
 [-0.61570883 -0.13198533 -0.50207895]]

So \(A_{i \neq k, j \neq k}\) is:

A_rem = A[1:S, 1:S]
print(A_rem)

[[-0.28067929  0.38998372]
 [-0.13198533 -0.50207895]]

And \(A_{i \neq k, k}\) is:

A_col = A[:, 0][1:S]
print(A_col)

[-0.00439125 -0.61570883]

Applying Eq. 15:

delta_eq_15 = np.linalg.inv(A_rem) @ A_col
print("Proportional change from Eq 15:")
print(delta)

Proportional change from Eq 15:
[1.25949637 0.89522531]

Both methods give the same \(\delta\), which verifies Eq. 15 is correct.

References

Bender, E. A., Case, T. J. and Gilpin, M. E. (1984). Perturbation experiments in community ecology: theory and practice, Ecology 65(1): 1–13.

Kristensen, N.P., Chisholm, R.A., McDonald-Madden, E. (2019) Dealing with high uncertainty in qualitative network models using Boolean analysis, Methods in Ecology and Evolution 10: 1048-1061

Nakajima, H. (1992). Sensitivity and stability of flow networks, Ecological Modelling 62(1): 123–133.

Raymond, B., McInnes, J., Dambacher, J. M., Way, S. and Bergstrom, D. M. (2011). Qualitative modelling of invasive species eradication on subantarctic Macquarie Island, Journal of Applied Ecology 48(1): 181–191.

Background to the paper

Kleshnina et al. (2023) studied an iterated Prisoner’s Dilemma (PD) where the actions of the players affect the environment and visa versa. Typically, if the environment is good, the players receive higher payoffs, but if some players defect, then the environment transitions from good to bad. They were interested in what effect knowledge of the environment’s state would have on cooperation outcomes. Here, however, I will focus on one small aspect of the methodology: how to identify if a strategy is a sub-game perfect Nash equilibrium and the conditions required. This is the focus of Supplementary Note 3.

Game structure

Two players are playing an iterated a Prisoner’s Dilemma (PD), where in each round they can either cooperate (C) or defect (D). The environment has two possible states, \(S = \{ s_1, s_2 \}\), or ‘good’ and ‘bad’, respectively. The environment state determines payoffs according to the tables below, where \(b_1 > b_2 > c\).

In the good environment:

In the bad environment:

Environment transitions

I will focus on the scenario where the environment is deterministic and changes state depending on its previous state and the players’ actions. In each round, the environment will either transition to the good state or the bad state. To represent this mathematically, let \(q_{a, \overline{a}}^i\) be an indicator variable given the previous environment state \(i\) and player actions \(a, \overline{a}\). When \(q_{a, \overline{a}}^i = 1\), the environment will transition to the good state in the next round; when \(q_{a, \overline{a}}^i = 0\), it will transition to the bad state. The complete set of possible transitions can be represented by the vector:

I will also focus on the full-information setting, where players actions depend on both the current environment state as well as the players’ previous actions (memory-1). Similar to the environment transitions, we use an indicator variable \(p_{a, \overline{a}}^j\) to represent a player’s decision in state \(j\) given previous actions \(a, \overline{a}\). Here, \(p_{a, \overline{a}}^j = 1\) indicates cooperation and \(p_{a, \overline{a}}^j = 0\) indicates defection. A player’s complete strategy can therefore be represented by the vector:

Player strategies

In Supplementary Note 3, Kleshnina et al. study what they call the ‘timeout’ game. In this game, if any player defects, both are penalised by spending one round in the bad environment. This mechanism can be represented by the transition vector:

They analyse several strategies in this setting, including one that combines two well-known approaches: playing ‘Grim’ in the good environment and ‘win-stay, lose-shift (WSLS)’ in the bad environment. This hybrid strategy is represented by the vector:

One-shot deviation analysis

Kleshnina used the one-shot deviation principle to determine when the Grim-WSLS strategy in the timeout environment is a sub-game perfect Nash equilibrium (SPNE). Her analysis examines every possible combination of previous actions and current environment state (e.g., (CC, good), (CD, good), (DC, good), …, (DC, bad), (DD, bad)). For each combination, we calculate:

• \(\pi_{a \overline{a}, i}\): the payoff for following the strategy
• \(\hat{\pi}_{a \overline{a}, i}\): the payoff for deviating from the strategy for one round
• \(\pi_{a \overline{a}, i} - \hat{\pi}_{a \overline{a}, i}\): the net benefit of staying with the strategy

For the strategy to qualify as a SPNE, it must always be more profitable to stick with the strategy than to deviate from it for even a single round. Mathematically, this means:

As an example, consider the payoffs of the non-deviating and deviating players starting at CC in the good environment. For the non-deviating case, if both players start at CC, then they will cooperate in all subsequent rounds. The payoff will be

where \(\delta\) is the probability of playing another round. Game theorists often use a \((1- \delta)\) normalisation to simplify the analysis. So the non-deviating payoff is calculated:

To calculate the one-shot deviation payoff, we calculate what the payoff would be if the focal player plays the opposite of what their strategy says for just one round, i.e., instead of C they play D, and the next round and then revert to their strategy.

The payoff in each round is tabulated below

The actual payoff is

which normalises to

Therefore, from the (CC, good) starting point, we obtain a condition for the strategy to be a SPNE

To simplify the condition, Kleshnina et al. take the limit as \(\delta \rightarrow 1\), which represents a kind of best-case scenario to identify a necessary condition. First we pull out common \(1-\delta\) terms

and as \(\delta \rightarrow 1\), the condition becomes

The analysis above is repeated for every possible combination (CC, good), (CD, good), …, (DD, bad). Kleshnina et al. find that the condition is satisfied for all other combinations except (DD, bad), which, in a similar way to (CC, good) above, results in a condition

Both of the conditions must be satisfied in order for the strategy to be a SPNE. However, we can simplify the analysis by determining relationship between the two conditions. Eq. 2 can be rewritten \(b_1 - c + 2 b_1 - b_2 - 2 c \geq 0\). Because \(b_1 > c\), we know that if Eq. 3 is satisfied, then Eq. 2 is satisfied. Therefore, Eq. 3 is the necessary condition for the strategy to be a SPNE.

Automating the analysis

In the kleshnina-2023-playground Github repository, I provide code that automates analysis above for an arbitrary environment \(\boldsymbol{q}\) and strategy \(\boldsymbol{p}\). Below, I will highlight some points of interests, and I also note areas that I’m uncertain about / could be improved.

Encoding the environment and strategy as a directed graph

I used NetworkX to encode every \((\boldsymbol{q}, \boldsymbol{p})\) as a directed graph. The nodes are the environment-state + action pairs, e.g., (CC, good), and the edges are the transitions between them. Fig. 1 below shows the Timeout-Grim-WSLS example from above.

Identifying attractors

In the Timeout-Grim-WSLS example above, the state (CC, good) is a steady state – once reached, players continue to cooperate and the environment remains good. However, it’s also possible to have periodic states that cycle through multiple configurations.

Consider an environment

and the strategy

As illustrated in Fig. 2 below, this system has three attractors:

1. A steady state or period-1 cycle: (CC, good) \(\rightarrow\) (CC, good) \(\rightarrow\) …
2. A period-2 cycle: (CD, bad) \(\rightarrow\) (DC, bad) \(\rightarrow\) (CD, bad) \(\rightarrow\) …
3. A period-3 cycle: (CC, bad) \(\rightarrow\) (DD, bad) \(\rightarrow\) (DD, good) \(\rightarrow\) (CC, bad) \(\rightarrow\) …

We need to identify such cyles, and we will find that the normalisation used above no longer applies.

To identify cycles, I used the strongly_connected_components() function from NetworkX. A strongly connected component (SCC) is a subgraph of a directed graph that has a path in each direction between each pair of vertices and is maximal with respect to this property. This function returns multi-node cycles plus SCCs of length 1. SCCs of length 1 may either be a node with no incoming links or a period-1 cycle. This is implemented in the find_cycles() function in fncs_general.py.

def find_cycles(G):

    # find the attractors using the strongly-connected components algorithm
    sccs = list(nx.strongly_connected_components(G))
    cycles = []
    for scc in sccs:
        if len(scc) > 1:
            # multi-node SCCs are always cycles
            cycles.append(scc)
        elif len(scc) == 1:
            node = list(scc)[0]
            # an SCC of size 1 is a steady-state iff it's a self-loop
            if G.has_edge(node, node):
                cycles.append({node})

    return cycles

Returning to our example in Fig. 2, we find that the normalisation factor \((1 - \delta)\) no longer applies. For example, the unnormalised no-deviation payoff from (CD, good) is

Therefore, when the payoffs are calculated in calc_longterm_payoffs() (in fncs_general.py), we leave them in their unnormalised form and perform the simplifications later when the conditions are evaluated (in SageMath, detailed below).

Calculating the no-deviation and deviation payoffs

I encoded the payoffs using SymPy (calc_one_shot_devns.py), and checked the conditions using SageMath (define_variables_assumptions.sage and check_spne.sage). To replicate the analysis done in Supplementary Note 3, I did the checking of the conditions incrementally, proceeding to the next step if the previous result was ambiguous.

1. Check the SPNE condition directly: Can SageMath immediately discern the sign of \(\pi_{a \overline{a}, i} - \hat{\pi}_{a \overline{a}, i}\)?
2. Use SageMath function numerator_denominator() to cancel the normalisation factors. Can SageMath discern the sign of each?
   • Note that I’m uncertain about the robustness of this step because it performs the simplifications I need as kind of side-effect of creating the fractional form and splitting it.
3. Simplify by setting \(\delta = 1\). Can SageMath discern the sign of \(\lim_{\delta \rightarrow 1} \pi_{a \overline{a}, i} - \hat{\pi}_{a \overline{a}, i}\)?
4. Write the condition from Step 3 to a file.

I found that SageMath had difficulty working in the \((b_1, b_2, c)\) parameter space, so I shifted to an \((x, y, c)\) parameter space defined as

with the constraints \(x, y > 0\).

I don’t feel very confident about the SageMath implementation. I made an attempt to rewrite it in Z3, but I ran into difficulties because Z3 does not have an equivalent to SageMath’s numerator_denominator() function. Perhaps I can use some combination of SymPy and Z3 for this step. This is an area for future improvement.

For each \(\boldsymbol{q}\), output was a CSV file (one_shot_devns_q_[binary string].csv):

Calculate the necessary conditions

For each strategy that had the potential to be a SPNE in environment \(\boldsymbol{q}\), I used the Z3 Theorem Prover to determine which of the conditions (arising from each (CC,good), (CD, good), etc.) were the necessary conditions. In other words, I am analysing the relationships between the expressions arising from the requirement \(\pi_{a \overline{a}, i} - \hat{\pi}_{a \overline{a}, i} \geq 0\), such as the condition \(3 b_1 - b_2 - 3 c \geq 0\) in the Timeout-Grim-WSLS example.

For each strategy, the initial steps were:

First, identify all unique conditions using are_equivalent() in fncs_z3_1.py:

def are_equivalent(condn_a, condn_b):
    """
    Returns True if condn_a and condn_b and equivalent.
    """

    s = Solver()
    s.add(condn_a != condn_b)
    result = s.check() == unsat

    return result

Second, check if the unique conditions are mutually satisfiable (in calc_necess_condns.py):

# earlier in the code, specify assumptions on parameters
b1, b2, c, d = Reals("b1 b2 c d")
variables = [b1, b2, c, d]
assumptions = And(
    d > 0,
    d <= 1,
    c > 0,  # b1 ≥ b2 > c
    b2 > c,
    b1 > b2, # NOTE I changed this from Maria's b1 >= b2
)

# for each strategies unique conditions ...

# check conditions' mutual satisfiability
s = Solver()
s.add(assumptions)
for condn in condns:
    s.add(condn)
result = s.check()

If the conditions were mutually satisfiable, I then identified the minimal set of conditions that were the necessary conditions for that strategy. For each pair of conditions \(C_1\) and \(C_2\), I used Z3’s qe Tactic to determine if \(C_1 \implies C_2\), implemented in check_implication():

# in the script that calls the function, specify we're using 'qe' tactic
tactic = Tactic("qe")

# for each pair of conditions, call this function
def check_implication(condn_a, condn_b, assumptions, variables, tactic):
    """
    Returns True if condn_a implies condn_b under the given assumptions
    """

    formula = ForAll(variables, Implies(And(assumptions, condn_a), condn_b))
    result = tactic.apply(formula)

    return result.as_expr()

This allowed me to construction an implications matrix, which has rows and columns corresponding to the conditions, and an entry 1 indicates that \(C_i \implies C_j\). The minimal set is the set of all conditions that are not implied by another condition, i.e., the independent roots of the implications tree.

The results were stored in CSV files necess_condns_q_[binary string].csv. The Timeout environment example (necess_condns_q_100111.csv) is shown below.

Grouping same-condition strategies

Often, different strategies \(\boldsymbol{p}\) have the same necessary conditions. To further summarise the analysis, I grouped all such \(\boldsymbol{p}\) together using PyEDA’s Boolean minimisation on the set of \(\boldsymbol{p}\) binary strings.

For example, in the Timeout environment, the \(\boldsymbol{p}\) corresponding to the following 4 binary strings have no additional conditions in order to be a SPNE:

00000000
00001000
10000000
10001000

These four strings can be represented in a more compact form by a single string

-000-000

where the - indicates that the strategy can either cooperate or defect in that state.

The Boolean minimisation was implemented in group_necess_condns.py and output was written to CSV files necess_condns_grouped_q_[binary string].csv. The Timeout environment example (necess_condns_grouped_q_100111.csv) is shown below.

I wrote scripts plot_necess_condns.py and plot_transn_graphs_pq.py to visualise each \(\boldsymbol{p}\) group and its necessary conditions. I found it more convenient to work in the \((x, y)\) parameter space for the conditions.

A summary of all SPNE in sensible environments

With code to automate the analysis, it is possible to do a sweep of a range of scenarios quickly. Below, I show the results I obtained for all environments with a ‘sensible’ transition pattern, i.e., that stay in or return to the good environment when both players cooperate and stay or return to the good environment when both players defect. These environments match the pattern

Figs. 4–6 below summarise the SPNE I found in each environmental scenario.

Environments are categorised based on how fragile they are and their return conditions. A fragile environment transitions from good to bad when any player defects, but a resilient environment only transitions when both players defect.

The conditions for return from the bad to good environment can be classified as:

1. harsh conditional – both players must cooperate,
2. conditional – at least one player must cooperate, or
3. timeout – returns regardless of what players do.

In all environments, a variation that always defects in the bad environment in response to any defection in the previous round is an unconditional SPNE.

All other potential SPNE are conditional and have (CC, good) as an attractor. In the resilient environment, they have in common a 100... pattern, which means that, if they are in the good environment, they respond to defection by the other in the previous round with a defection.

A strategy that defects in the bad environment when the previous action was DD is only ever a potential SPNE in the timeout environment. The strategy with the weakest necessary condition is such a strategy, and it occurs in the resilient environment.

In the Github repository, I also have results for \(\boldsymbol{q} = (1, -, 0; 1, 0, 1)\). I call this a ‘strange return’ because the bad environment improves when both players defect. Perhaps unsurprisingly, some of the strategies and conditions it finds are quite different from those above, and we can visualise those results similar to the ‘sensible’ environment above and puzzle over what they mean.

References

Kleshnina, M., Hilbe, C., Šimsa, Š., Chatterjee, K. and Nowak, M.A., 2023. The effect of environmental information on evolution of cooperation in stochastic games. Nature Communications, 14(1), p.4153.

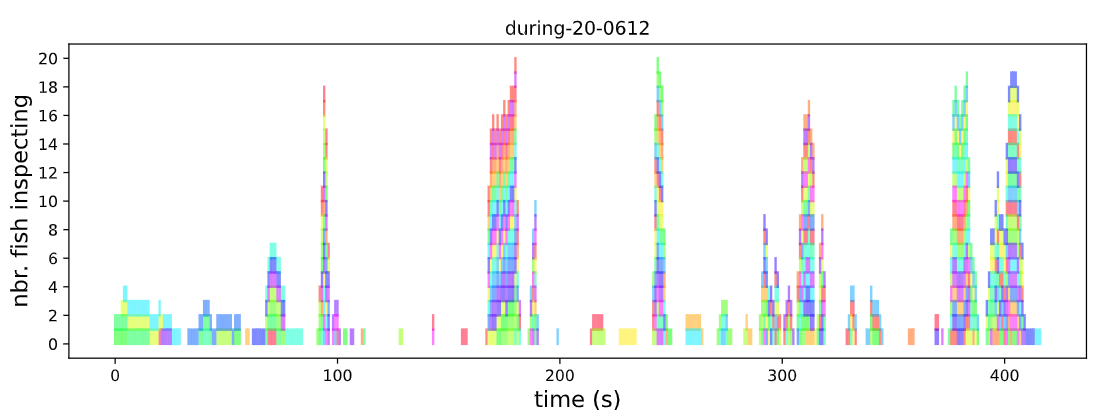
To learn more about the evolution of cooperation from a philosopher’s perspective, I recently read Richard Joyce’s book The Evolution of Morality. Joyce’s book makes the case for the evolutionary debunking argument, which holds that moral beliefs are the product of evolutionary processes rather than tracking moral truths. While evolution has equipped us with the capacity for moral judgement, this doesn’t necessarily mean that our moral beliefs are true or justified. Instead, our moral sense evolved because it was useful for our ancestors’ survival and reproduction, regardless of whether moral facts actually exist.

Joyce begins by examining the evolutionary origins of helping behaviour, drawing on mechanisms familiar to evolutionary game theorists such as kin selection and mutualism. He proposes that emotions originally directed towards kin were co-opted for broader prosocial purposes. However, he argues this evolutionary account of helping behaviour falls well short of explaining morality in its full sense (Chapter 2). Even if humans had hypothetically evolved to behave in extremely altruistic ways, this alone would not constitute morality proper. The key distinction lies in the capacity for moral judgement. A creature could evolve with extreme inhibitions against behaviours we consider immoral, but without the concept of prohibitions and the ability to make moral judgements, it would not possess true morality.

This distinction leads Joyce to grapple with what moral judgement truly is. Some philosophers consider morality conative, suggesting statements like “Stealing is wrong” are akin to exclaiming “STEALING!!” in an angry voice, expressing disapproval rather than a factual claim. However, Joyce contends that moral judgements also involve cognitive beliefs. To support this argument, he employs Moore’s paradox sentences such as “Stealing is wrong, but I don’t believe it’s wrong”. The apparent contradiction arises because moral judgements also seem to express a cognitive belief. (His later discussion of moral projectivism also makes a compelling argument.)

A second distinctive property of moral judgements is their clout. Compare “I disapprove of fox hunting” to “Fox hunting is wrong”; the latter has much more ‘oomph’ than the former. When someone declares that fox hunting is wrong, they’re not merely expressing a personal preference, they’re making a claim that demands consideration from their audience regardless of the audience’s attitude towards the speaker or personal interests.

In Chapter 3, Joyce presents a contentious argument that non-human animals lack the capacity for moral judgement. He acknowledges that chimpanzees, for example, demonstrate complex social rules governing accepted and unaccepted behaviours (de Waal 1991). However, he argues these behaviours can be fully accounted for by aversions, inhibitions, and desires. He draws a distinction between these responses and the more sophisticated concept of acceptable and unacceptable behaviours, which involves evaluative concepts like transgression, prohibitions, and deserved punishment.

Joyce’s main argument for the absence of moral judgement in other animals hinges on the role of language, a stance he acknowledges is controversial among philosophers. He focuses on the concept of “thick evaluative terms” to illustrate his point. These are words like “kraut” that carry both a descriptive component (“German”) and an evaluative one (derogatory). Understanding such terms requires a “semantic ascent” — the ability to shift from discussing the subject to analysing the term itself — which requires metalinguistic knowledge. Joyce argues that while other animals might grasp descriptive concepts like “German”, they lack the linguistic capacity for evaluative concepts like “kraut”. This linguistic limitation prevents other animals from making true moral judgements. Consequently, what we might perceive as “punishment” among other animals is more accurately described as a “negative response”.

He acknowledges some readers might be unpersuaded by his argument, but a key question remains for us all: how does one move from having inhibitions to making judgements about prohibitions?

Joyce speculates that language may have evolved, in part, to facilitate the expression of evaluations, with gossip and indirect reciprocity playing pivotal roles. He argues that when we tell others about someone who cheated us, our goal isn’t to merely describe the event, but to criticise the action and potentially elicit a response from the listener.

Building on this, Joyce explores how many moral emotions are not only dependent on evaluative concepts but are also cognitively rich. He uses disgust as a prime example. While its biological root lies in food rejection, humans have elaborated this basic instinct into complex, almost superstitious beliefs. For example, people might refuse to wear a murderer’s jumper even after thorough laundering, revealing a concept of contamination that transcends physical reality. Joyce argues that while infants and non-human animals can experience distaste, they lack access to the full concept of disgust with its notions of invisible contaminants and realities distinct from appearance. Similarly, he examines guilt as another cognitively rich moral emotion. True guilt involves the concept that punishment is deserved rather than merely fearing or expecting it. While a dog might display guilt-like behaviour when acting submissively after wrongdoing, Joyce classifies this as proto-guilt, distinct from guilt proper.

In Chapter 4, Joyce examines the evolutionary benefits of self-directed moral judgement. He argues that moral conscience evolved as a more robust mechanism for scenarios where prudential judgement is too flexible and error-prone (e.g., “I should eat this salad for my future health”). Moral conscience says an action must be performed, silencing further deliberation, and it provides a strong motivation akin to how orgasm incentivises sex.

A key evolutionary advantage of moral judgement is its ability to unite self-directed and other-directed evaluations, serving as a ‘common currency’ for collective decision-making. Self-directed judgements act as a motivational bulwark, but they can also be publicly asserted, e.g., when staking a claim. The declaration ‘X is morally wrong’ demands avoidance from both the speaker and the audience. But because moralised thinking is motivationally resolute, it can also function as an interpersonal commitment. Emotions like indignant anger guarantee the pursuit of justice even at personal cost, which can be in one’s self-interest if it can be communicated to others.

Empirical evidence suggests that moral judgement is facilitated by emotions. Joyce argues for moral projectivism, drawing an analogy with colour perception. Just as we project the qualia of ‘red’ onto objects, we project emotions like pity onto situations, perceiving them as objective features (a pitiful situation) rather than subjective responses. This view can be contrasted with the traditional notion that moral judgements involve perceiving objective moral facts that exist independently in the world. While not definitively proven, moral projectivism aligns with our understanding of sensory perceptions and is consistent with two key features of morality: the precedence of emotions in moral judgement (as demonstrated in experiments manipulating disgust), and the perception that moral attributes exist objectively, which emerges in early childhood.

In contrast, Joyce finds it difficult to explain how moral judgements could be purely learnt. He questions how abstract concepts like ‘moral transgression’ could be taught through punishment alone, or how children could infer the distinction between moral and conventional rules without wide exposure to the full range of cases necessary to make the inference (e.g., an authority changing their mind about a moral transgression). Instead, he argues that, while the content of the moral judgement may be learnt, moral judgement itself is innate.

In Chapter 5, Joyce examines attempts to vindicate morality, beginning with the distinction between global naturalism and moral naturalism. He illustrates this difference using an analogy: one could ‘naturalise witchcraft’ by providing sociological and anthropological accounts without asserting the existence of witches. Similarly, one could offer a scientifically respectable account of morality without claiming moral beliefs are true. Moral naturalism, however, goes further to assert that moral properties and relations genuinely exist.

The naturalistic fallacy, while not applicable to global naturalism, is often considered a significant challenge to moral naturalism. However, Joyce notes that the common understanding of the “naturalistic fallacy” — deriving an “ought” from an “is” — differs from its original meaning. He clarifies G.E. Moore’s initial argument, which is that ‘good’ is indefinable due to its simplicity. Moore contended that ‘good’, akin to ‘yellow’, lacks constituent parts and therefore resists decompositional definition (unlike, say, “horseness” = quadruped + gramnivorous + …). This argument is distinct from the issue of deriving ‘ought’ from ‘is’.

Addressing the derivation of ‘ought’ from ‘is’, Joyce argues that moral naturalism doesn’t necessarily violate this principle. He draws a parallel with how tables and chairs can be understood within the framework of physics: moral naturalists could potentially demonstrate that moral properties are either identical to or supervene upon natural properties. While this task is challenging, Joyce suggests it shouldn’t be dismissed outright as impossible.

Joyce contends that evolutionary vindications of morality often falter for two primary reasons. First, many advocates propose an instrumentalist form of justification, which opens the door to the possibility that moral beliefs are merely “useful fictions”. This approach fails in Joyce’s view because he adheres to partial cognitivism, maintaining that moral beliefs are genuine beliefs. Second, those who offer epistemic justifications tend to employ non-normative definitions of “ought” (e.g., equating “ought” with “will happen”) that consequently fail to account for morality’s inherent clout.

Joyce then proceeds to examine several proposals in detail:

1. Richards (1986) argues that all justifications must eventually reach a stopping point, such as the modus ponens in logical arguments. He suggests that just as modus ponens derives its validity from the beliefs and practices of rational people, the transition from “is” to “ought” can be justified by examining the beliefs and practices of moral people.

   Joyce counters this by suggesting it would be more logical to look to rational, rather than moral, people. He questions whether modus ponens is truly justified solely by appealing to rational judgement and points out that widespread assent doesn’t equate to an inference rule.

   Richards also attempts to vindicate morality by proposing that evolution has adapted us to act for the community’s good, which he equates with morality.

   Joyce, while accepting this premise for argument’s sake, contends through counter-examples that community good isn’t synonymous with morality (e.g., Genghis Khan’s henchmen acted for their community’s good). Moreover, he argues that even if one accepts this equivalence, evolutionary considerations at best suggest that humans will act to benefit the community, not that they ought to.

2. Campbell (1996) contends that morality is justified because it improves people’s lives.

   Joyce critiques this, arguing that Campbell employs an incorrect notion of justification. He draws a parallel with religious belief: while it might improve lives, does that epistemically justify believing in gods? Joyce asserts that while this might provide instrumental justification, it falls short of the epistemic justification required for beliefs.

   Campbell further argues that epistemic justification is inappropriate for morality, claiming that moral beliefs are distinctive not in their subject matter, but in being essentially dispositions to think, feel, and act in certain ways.

   Joyce acknowledges that Campbell’s position is coherent, but only if morality is construed non-cognitively. He maintains that if moral beliefs are indeed beliefs, they must be subject to epistemic scrutiny.

3. Dennett (1995) posits that moral judgement plays a crucial practical role, and suggests that its efficacy might require avoiding excessive reflection on its functioning.

   Joyce notes that the first part of Dennett’s argument is an instrumental justification, similar to Campbell’s position. Regarding the second point, Joyce interprets Dennett as potentially advocating a form of moral fictionalism, to which he is sympathetic. This view holds that while moral judgements may not be true, and we can acknowledge this, it remains beneficial to treat them as true in our daily lives.

4. Casebeer (2003) proposes a neo-Aristotelian account of virtue, where human purpose is understood in Darwinian terms. While evolution provides a framework to discuss the purposes of specific organs like hands or eyes, it doesn’t assign an obvious function to humans as a whole, so one might bridge this gap by using a concept like ‘organism flourishing’.

   Joyce critiques this approach on several grounds. Firstly, he argues that a value system based on self-interest and harm avoidance doesn’t constitute a moral system in the traditional sense. He draws an analogy: we don’t praise a heart for pumping blood well, nor an assassin for excelling at their profession. Thus, evolution doesn’t provide a basis for moral ‘good’, even if such evaluations align with Aristotelian virtue ethics.

   Furthermore, Joyce invokes Mackie’s observation about the ‘queerness’ of moral properties. If moral properties exist, they imbue situations with demands for certain actions, regardless of an individual’s personal aims, and these demands derive authority from no human source, existing merely to be perceived by moral agents. Joyce argues that Casebeer’s approach doesn’t resolve this metaphysical issue. Just as a heart’s function to pump blood doesn’t imply a demand that it must do so, identifying a function for humans wouldn’t inherently create a moral imperative to fulfil it.

In the final chapter, Joyce addresses the evolutionary debunking of morality. He begins with a thought experiment: if you discovered you had been given a pill that made you believe Napoleon lost at Waterloo, wouldn’t that make you doubt this belief? Joyce argues that the discovery that our moral beliefs are products of evolution should prompt a similar doubt.

One might counter that natural selection tends to produce true beliefs. For example, if the belief that 1+1=2 were innate and evolved, its evolutionary origin wouldn’t invalidate it because its selective advantage stems from its truth. The same argument could be applied to the faculties of scientific inquiry that underpin the evolutionary debunking of morality itself. However, drawing on Harman (1977, 1986), Joyce contends that this reasoning doesn’t hold for moral beliefs. We can understand how moral beliefs evolved and benefited our ancestors without those beliefs necessarily being true. While “right” and “wrong” might denote something real about the world, they might do so in a manner akin to terms like “ghost” or “witch”.

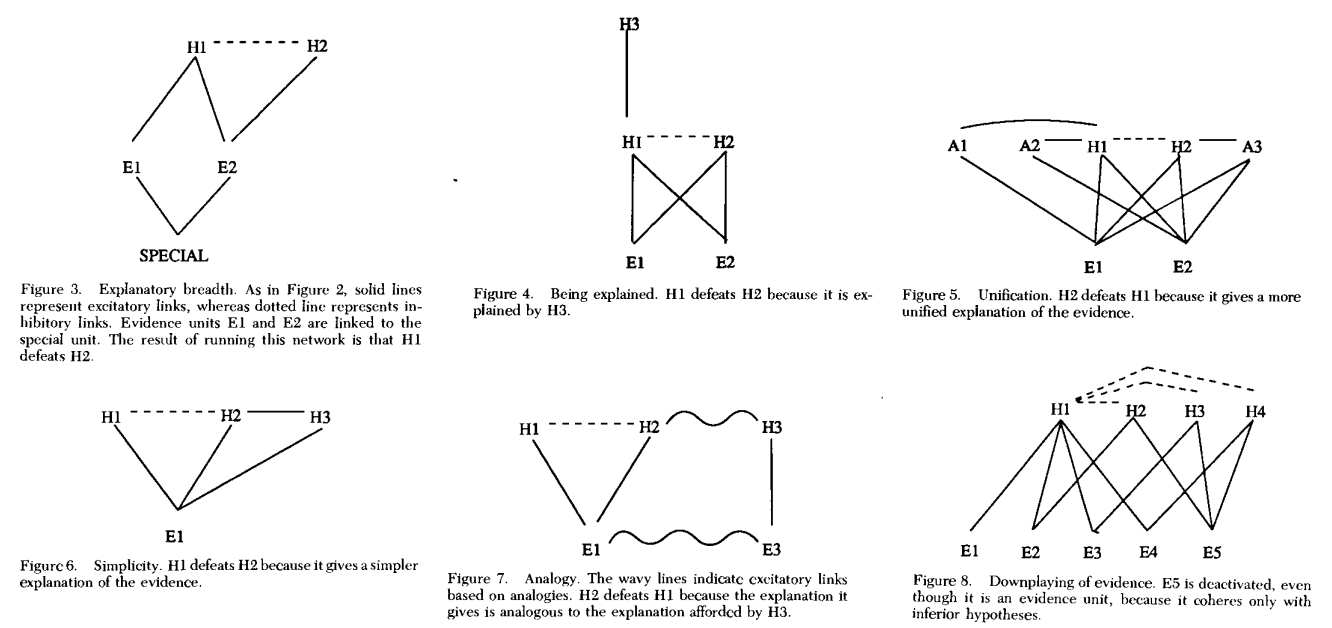
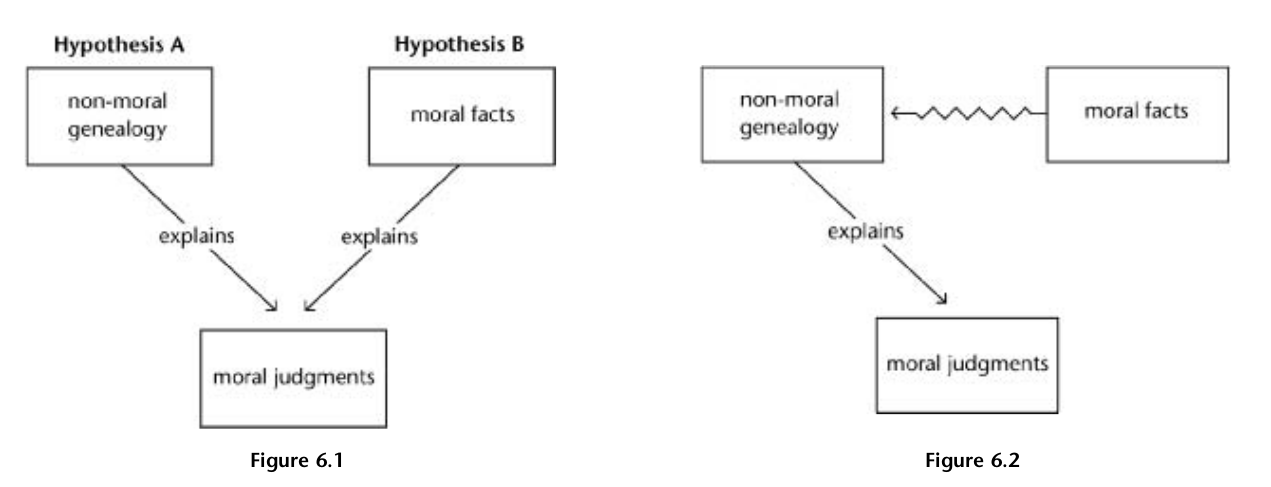
If a non-moral genealogy can fully explain moral judgement, the onus falls on moral naturalists to demonstrate why moral facts aren’t redundant (Fig. 6.1). This would require a reductive account that explains how moral facts relate to natural ones. Consider a hypothetical scenario: Jane sees children setting fire to a cat and judges it wrong. Can we explain Jane’s judgement without invoking the concepts of “cat”, “burning”, and “wrongness”? The concepts of “cat” and “burning” can be reduced to physics, so they’re implicitly present in that part of the causal explanation. However, if we can provide a naturalistic explanation for why the situation merely seemed wrong to Jane, we don’t need to posit the actual existence of wrongness to explain her judgement.

What constitutes an adequate reduction can be quite broad. While it’s challenging to move directly from physics and chemistry to concepts like “cat” and “burning”, we do have an account explaining how a burning cat is a physical and chemical entity. If a similar account can be provided for how moral facts are naturalistic entities, the critique would be satisfied (Fig. 6.2). However, to be credible, such an account would need to be as concrete and precise as a successful theory positing the existence of witches.

Joyce focuses on one key challenge facing moral naturalists: accounting for the inescapable practical authority that moral claims seem to possess. He chooses this example to illustrate a key point: if even a theory that equates moral facts with facts about reason can’t sufficiently explain this authority, what hope is there for theories that make this connection only indirectly?

The question becomes: how can naturalistic facts account for the clout of moral values? Essentially, we’re searching for a type of reason for action that can explain moral authority. Joyce examines two approaches:

1. Practical reasoning theory posits that an act is wrong if the agent has sufficient reasons not to do it. However, this theory falls short in explaining the inescapability of moral clout, which should have authority over people regardless of their personal interests.

2. The self-conception strategy argues that a rational person must treat morality as authoritative to maintain a coherent self-conception (e.g., a sense of integrity and identity). Yet this approach also has limitations. The reasons for action still depend on our actual desires, and the intangibility of the supposed self-harm caused by immoral actions is problematic. While some proponents describe the consequences of immoral actions in catastrophic terms (e.g., losing self-value), this seems disproportionate for minor transgressions like nicking a pen, which the theory must also account for.

Some philosophers argue that clout is not a necessary feature of morality. However, Joyce contends that without this authoritative element, morality would function more like etiquette– a set of contingent rules rather than absolute imperatives. Even steadfast desires, he argues, are insufficient to capture the essence of moral judgements. Joyce questions what the notion “X is morally wrong” adds to an account based solely on likes and dislikes. He had previously argued that moral discourse is necessary because it acts as a bulwark in ways that non-moralised practical deliberation cannot. However, this function is unavailable to proponents of moral naturalism who reject the notion of moral clout. Moreover, admitting moral discourse is superfluous would be inconsistent with moral realism, creating a dilemma for those who seek to maintain moral naturalism without the element of inescapable authority.

As an alternative to metaphysical theories, Joyce considers epistemic approaches that might vindicate moral beliefs regardless of their ontological status:

1. Process reliabilism holds that beliefs are justified when produced by processes that reliably link belief with truth, e.g., if natural selection favours organisms with at least approximately true innate beliefs. However, this approach faces two problems. First, the generality problem of specifying which is the relevant process (e.g., natural selection or specific cognitive mechanisms). Second, the deeper issue that natural selection may not always favour true beliefs, especially for intangible concepts like morality (cf., creation myths). The established existence of such beliefs also forces us to conclude that we’re faced with an unreliable process.

2. Epistemic conservatism holds that existing beliefs are rational unless proven otherwise. However, Sinnott-Armstrong (2006) identifies five attributes that can cast doubt on beliefs (a belief is partial, controversial, emotional, subject to illusion, and has unreliable/disreputable sources), including being explicable by unreliable sources, which applies to moral beliefs.

3. Epistemic coherentism suggests beliefs are justified by fitting coherently with other beliefs. However, when we include beliefs about the evolutionary origin of moral beliefs, which not only favour dropping a moral belief but also gives a scientifically respectable explanation for why the error occurred in the first place, then doubt is cast on the moral beliefs by coherentism’s own rules.

4. Moral intuitionism, a form of foundationalism, holds that some moral truths are self-evident. While this aligns with common intuitions about morality, items from Sinnott-Armstrong’s list (e.g., consider framing effects) again apply. More to the point would be to ask why moral beliefs seem beyond question and seem not to need further justification, to which the evolutionary geneology provides a good answer.

Thoughts

Joyce’s analysis has clarified for me a distinction in my research on the evolution of cooperation: while I’m seeking to explain cooperative behaviour, that falls short of addressing morality proper, which fundamentally involves judgement. The closest parallels are perhaps found in reputation models (indirect reciprocity), where rules emerge that align with our intuitions of “good” and “bad” behaviour (Ohtsuki and Iwasa 2004). However, even these models don’t fully capture the cognitive component and clout that Joyce identifies as essential to moral judgements.

Joyce’s emphasis on the role of clout suggests that before we can adequately model moral judgements, we need robust models of resolve and its failures. The concept of morality as an interpersonal commitment is particularly intriguing. It made me think of Sigmund et al.’s (2010) model of institutional punishment, though their model externalises commitment through pre-payment of taxes rather than internalising it. My own work on internal commitment in public goods games (in preparation, but similar to Newton’s (2017) threshold-PGG example) touches on related themes, but the commitment modelled there, being in the self-interest of collaborators, lacks the clout-bearing quality Joyce describes in true moral judgements.

I found it surprising that the primary challenges to moral naturalism centred on finding epistemic (rather than instrumental) justifications and employing a normative instead of descriptive version of “ought”. However, these challenges become more understandable in light of Joyce’s emphasis on cognitivism and clout. The concept of moral projectivism, with its clear analogy to qualia and sensory projection, struck me as particularly compelling.

References

Campbell, R., 1996. Can biology make ethics objective?. Biology and Philosophy, 11, pp.21-31.

Casebeer, W.D., 2003. Natural Ethical Facts: Evolution, Connectionism, and Moral Cognition. MIT Press.

de Waal, F.B., 1991. The chimpanzee’s sense of social regularity and its relation to the human sense of justice. American Behavioral Scientist, 34(3), pp.335-349.

Dennett, D.C., 1995. Darwin’s Dangerous Idea. Simon and Schuster.

Harman, G., 1977. The Nature of Morality: An Introduction to Ethics. Oxford University Press.

Harman, G., 1986. Moral explanations of natural facts—Can moral claims be tested against moral reality?. The Southern Journal of Philosophy, 24(S1), pp.57-68.

Joyce, R., 2006. The Evolution of Morality. MIT press.

Ohtsuki, H. and Iwasa, Y., 2004. How should we define goodness?—reputation dynamics in indirect reciprocity. Journal of theoretical biology, 231(1), pp.107-120.

Richards, R.J., 1986. A defense of evolutionary ethics. Biology and Philosophy, 1(3), pp.265-293.

Sigmund, K., De Silva, H., Traulsen, A. and Hauert, C., 2010. Social learning promotes institutions for governing the commons. Nature, 466(7308), pp.861-863.

Sinnott-Armstrong, W., 2006. Moral intuitionism meets empirical psychology. In Metaethics after Moore, ed. T. Horgan and M. Timmons. Oxford University Press.

This inclination towards coherent beliefs contrasts sharply with foundationalist approaches to knowledge, which advocate building beliefs from self-evident truths (e.g., Descartes’ “I think; therefore, I am”). Our belief systems instead resemble intricate webs, characterised by complex interdependencies rather than clear hierarchies. Coherence-based reasoning is a cognitive model that attempts to capture these realities of human thought, where our beliefs are formed and held within this interconnected framework. This model not only describes how we form new beliefs but also how we maintain and adjust our existing belief systems in the face of new information.

Experimental evidence supports the key hypotheses of coherence-based reasoning, showing that incipient conclusions can change how evidence is weighted. For example, in an experiment where participants were asked to judge a legal case, their evaluation of the evidence shifted to align with their eventual conclusions (e.g., Fig. 1). This ‘coherence shift’ phenomenon underscores the bidirectional nature of human reasoning processes.

Coherence-based reasoning, a Gestaltian cognitive-consistency model of human reasoning (reviewed in Simon and Read (2023)), is founded on the observation that we tend to accept propositions that align with our existing beliefs and reject those that contradict them. This theory, as formalised by Thagard (1989) in the ECHO (Explanatory Coherence by Harmony Optimisation) model, offers a compelling alternative to unidirectional theories of reasoning such as Bayesian inference. Proponents of coherence-based reasoning, like Simon et al. (2004), argue that the theory’s ability to capture ‘coherence shifts’ – such as those observed in the legal judgement experiment described earlier — makes it a more accurate representation of human cognitive processes (see also: Simon (2004); Glöckner and Betsch (2008)).

The ECHO model, proposed by Thagard (1989), formalises coherence-based reasoning using a connectionist framework. This model can be simulated using neural network techniques (e.g., Fig. 2) and consists of the following elements:

1. Nodes: Represent individual pieces of evidence and hypotheses.
2. Weighted edges: Signify relationships between nodes.
   1. Positive weights: Indicate explanatory links between hypotheses and evidence, co-hypotheses, or analogical connections.
   2. (b) Negative weights: Represent contradictions between hypotheses.

This network structure allows the model to simulate the complex interplay between different pieces of information and beliefs, mirroring the web-like nature of human cognition. By observing how activation spreads through a network, we can gain insights into how people might integrate new information, resolve contradictions, and ultimately form coherent belief systems.

Example

Consider the network structure illustrated in Fig. 3a, adapted from Fig. 8 of Thagard (1989). This network represents a scenario with five pieces of evidence (E1 to E5) and four hypotheses (H1 to H4). The relationships between these elements are as follows:

1. Hypothesis H1 exclusively explains evidence E1 and also accounts for E2, E3, and E4.
2. Evidence E5 is not explained by H1 but can be explained by hypotheses H2, H3, and H4.
3. Hypotheses H2, H3, and H4 each explain only one additional piece of evidence besides E5.
4. Hypotheses H2, H3, and H4 are mutually exclusive with H1, indicated by dashed lines.
5. A ’special’ node represents data priority, connected to all evidence nodes.

To simulate this model, activation propagates from the data to the evidence nodes, which in turn activate their connected hypothesis nodes. The nodes then influence each other based on their positive (solid lines) or negative (dashed lines) relationships. This process continues until the system reaches a steady state, representing the final decision regarding the believability of the hypotheses and evidences.

The simulation requires setting initial weights for the links between nodes. Following Thagard (1989), I used the default weightings:

• \(w_{ij} = 0.05\) for excitatory links, and
• \(w_{ij} = -0.2\) for inhibitory links.

These weightings may by modified to penalise the complexity of an explanation and to adjust the weighting of analogical links (no analogical links in this example).

The model is simulated as follows.

1. Initialise the `data priority’ node’s activation level \(a_0 = 1\) and all other nodes at some small initial value (default \(a_i = 0.001\)).
2. For each timestep, update all nodes \(j > 0\) while keeping data-priority node constant at \(a_0 = 1\):

   1. For each evidence and hypothesis node \(j\), calculate the net input to that node from all other nodes \(i\) connected to it

      \[\text{net}_j = \sum_i w_{ij} a_i \label{E:net_j}\]

   2. For each evidence and hypothesis node \(j\), update the node’s activation level \(a_j\) according to

      \[a_j(t+1) = a_j(t) (1 - \theta) + \begin{cases} \text{net}_j (\text{max} - a_j(t)) & \text{if } \text{net}_j > 0, \\ \text{net}_j (a_j(t) - \text{min}) & \text{otherwise.} \end{cases} \label{E:a_j_update}\]

      where max is the maximum node activation (default \(\text{max} = 1\)), min is the minimum node activation (default \(\text{min} = -1\)), and \(\theta\) is an activation decay parameter (default \(\theta = 0.05\)).

3. Repeat Step 2 until the maximum absolute change in activation level of any node falls below a set tolerance (default \(\text{tol} = 0.001\)).

Fig. 3b illustrates how the activation levels of selected nodes in our example change over time. For example, the activation level of hypothesis H1 increases over time while all others H2-H4 decrease below zero. This represents the process of arriving at the conclusion that H1 is true and the other hypotheses false.

Notably, the example also illustrates the potential for evidence suppression. Although E5 is an established piece of evidence, its activation decreases over time. This occurs because E5 only supports the less favoured hypotheses H2-H4, which are ultimately rejected by the model.

Thagard (1989) explains the rationale between this counter-intuitive behaviour:

Principle 4 [of his 7 principles of explanatory coherence] asserts that data get priority by virtue of their independent coherence. But it should nevertheless be possible for a data unit to be deactivated. We see this both in the everyday practice of experimenters, in which it is often necessary to discard some the data because they are deemed unreliable (Hedges 1987), and in the history of science where evidence for a discarded theory sometimes falls into neglect (Lauden 1976).

Final thoughts

While we often view evidence suppression as a cognitive flaw, the model and example above suggests it may be an emergent property of an otherwise adaptive mechanism. Our ability to discount or deactivate certain pieces of information, like E5 in the example above, enables us to form coherent, actionable beliefs in a world of noisy, often contradictory data. This process isn’t about wilfully ignoring evidence, but rather about contextualising it within a broader explanatory framework.

While this coherence-seeking tendency can be advantageous in many real-world scenarios, it may also underlie problematic cognitive biases such as confirmation bias or belief perseverance. Understanding this dual nature of coherence-based reasoning — its adaptive value and potential pitfalls — offers a rather nuanced view of human cognition, and may lead to more sophisticated models of reasoning and decision-making.

References

Glöckner, A. and Betsch, T. (2008). Modeling option and strategy choices with connectionist networks: Towards an integrative model of automatic and deliberate decision making, Judgment and Decision making 3(3): 215–228.

Simon, D. (2004). A third view of the black box: Cognitive coherence in legal decision making, University of Chicago Law Review 71: 511.

Simon, D. and Read, S. J. (2023). Toward a general framework of biased reasoning: Coherence-based reasoning, Perspectives on Psychological Science p. 17456916231204579.

Simon, D., Snow, C. J. and Read, S. J. (2004). The redux of cognitive consistency theories: evidence judgments by constraint satisfaction, Journal of Personality and Social Psychology 86(6): 814.

Thagard, P. (1989). Explanatory coherence, Behavioral and Brain Sciences 12(3): 435–467.